Метод непосредственного интегрирования
Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется не посредственным интегрированием.
При сведении данного интеграла к табличному часто используются следующие преобразования дифференциала (операция «подведения под знак дифференциала»):
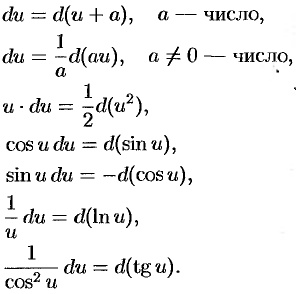
Вообще, 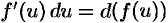 , эта формула очень часто используется при вычислении интегралов.
, эта формула очень часто используется при вычислении интегралов.
Примеры:
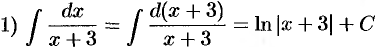 (формула 2 таблицы интегралов);
(формула 2 таблицы интегралов);
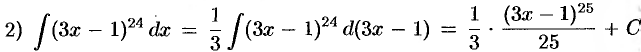
(формула 1);
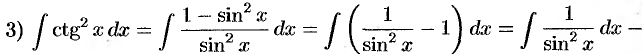
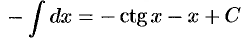 (формулы 10 и 1);
(формулы 10 и 1);
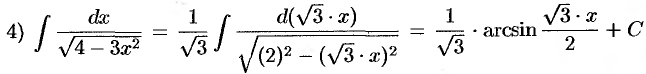
(формула 13);
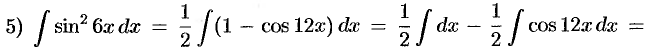
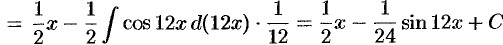 (формулы 1 и 6);
(формулы 1 и 6);
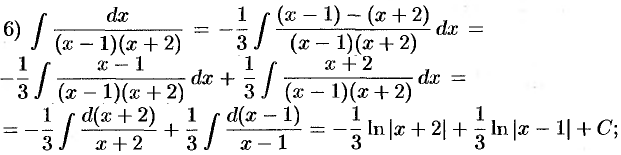
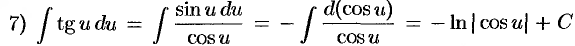 (вывод формулы 7);
(вывод формулы 7);
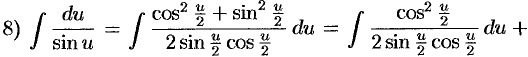
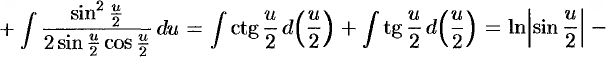
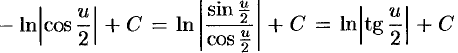 (вывод формулы 11);
(вывод формулы 11);
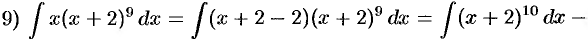
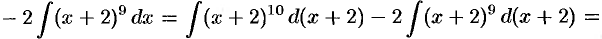
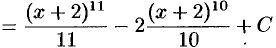 (формула 1);
(формула 1);
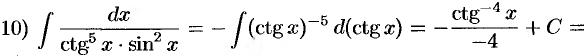
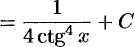 (формула 1);
(формула 1);
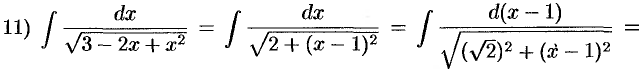
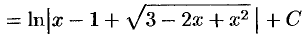 (формула 14);
(формула 14);
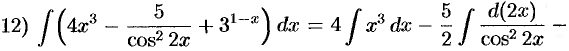
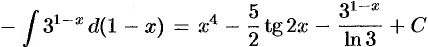 (формулы 1, 9, 3);
(формулы 1, 9, 3);
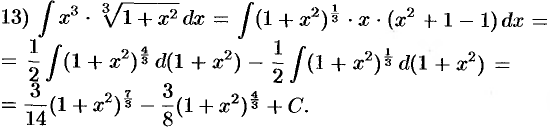
Как видно, вычисление интегралов иногда требует некоторой изобретательности, так сказать, «индивидуального подхода к каждой подынтегральной функции».
Соответствующие навыки приобретаются в результате значительного числа упражнений.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Свойства неопределенного интеграла |
| Таблица неопределенных интегралов |
| Метод интегрирования подстановкой |
| Метод интегрирования по частям |

