Оглавление:
Формула Тейлора для многочлена
Пусть функция 
есть многочлен 
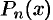степени 
:
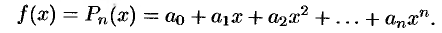
Преобразуем этот многочлен также в многочлен степени относительно разности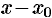 
, где 
— произвольное число, т. е. представим 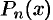в виде
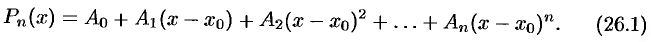
Для нахождения коэффициентов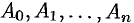 
продифференцируем раз равенство (26.1):
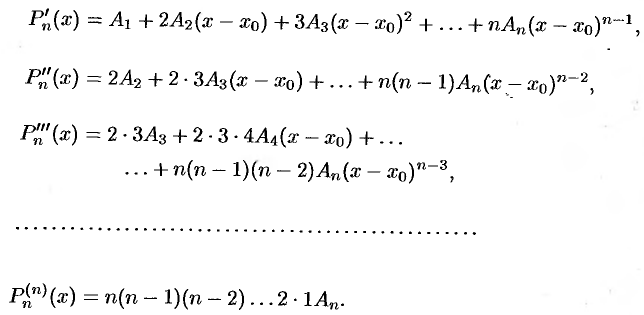
Подставляя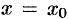 
в полученные равенства и равенство (26.1), имеем:
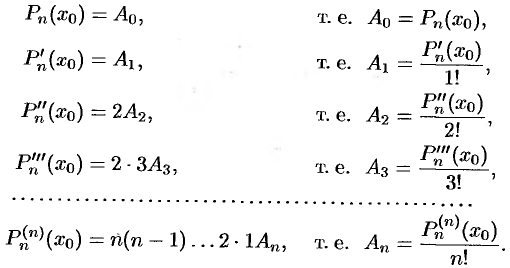
Подставляя найденные значения 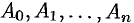в равенство (26.1), получим разложение многочлена -й степени 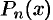по степеням ():
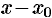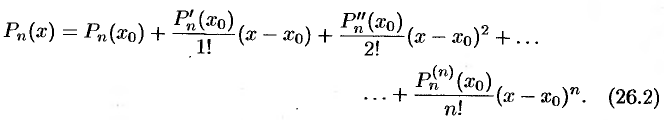
Формула (26.2) называется формулой Тейлора для многочлена 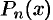степени .
Пример №26.1.
Разложить многочлен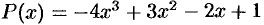 
по степеням 
.
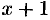Решение:
Здесь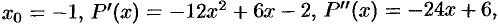 
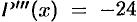. Поэтому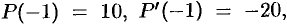 
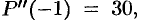
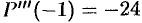. Следовательно,
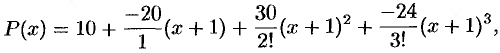
т. е.
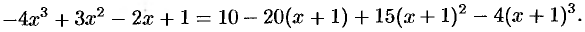
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Раскрытие неопределенностей различных видов |
| Формула Тейлора для функции |
| Формула Тейлора для произвольной функции |
| Геометрическое изображение комплексных чисел |
