Оглавление:
Раскрытие неопределенностей различных видов
Правило Лопиталя применяется для раскрытия неопределенностей вида 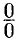 и
и 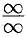 , которые называют основными. Неопределенности вида
, которые называют основными. Неопределенности вида 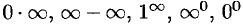 сводятся к двум основным видам путем тождественных преобразований.
сводятся к двум основным видам путем тождественных преобразований.
1. Пусть 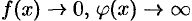 при
при  . Тогда очевидны следующие преобразования:
. Тогда очевидны следующие преобразования:
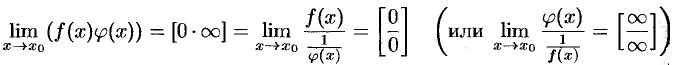
Например,
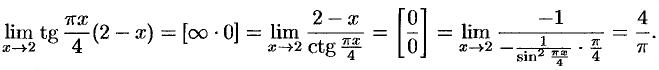
2. Пусть 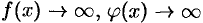 при
при  . Тогда можно поступить так:
. Тогда можно поступить так:
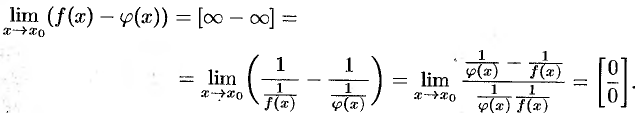
На практике бывает проще, например,
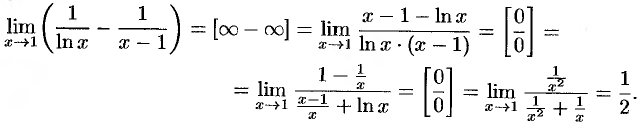
3. Пусть или 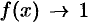 и
и 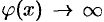 , или
, или 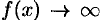 и
и 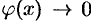 , или
, или 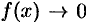 и
и 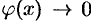 при
при  . Для нахождения предела вида
. Для нахождения предела вида 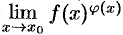 удобно сначала прологарифмировать выражение
удобно сначала прологарифмировать выражение
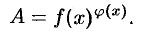
Пример №25.5.
Найти 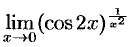 .
.
Решение:
Имеем неопределенность вида 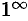 . Логарифмируем выражение
. Логарифмируем выражение 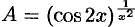 получим:
получим: 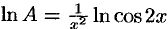 . Затем находим предел:
. Затем находим предел:
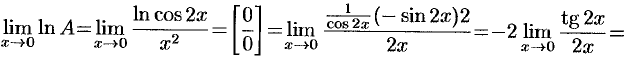
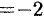 , т.е.
, т.е. 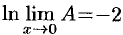 . Отсюда
. Отсюда 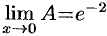 , и
, и 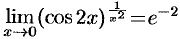 .
.
Решение можно оформить короче, если воспользоваться «готовой» формулой
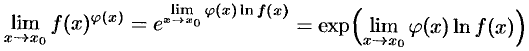
(использовано основное логарифмическое тождество: 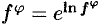 ).
).
Дополнительные примеры:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Гиперболические функции и их производные |
| Правило Лопиталя и раскрытие неопределённостей |
| Формула Тейлора для функции |
| Формула Тейлора для многочлена |

