Оглавление:
Правила Лопиталя
Рассмотрим способ раскрытия неопределенностей вида 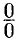 и
и 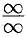 , который основан на применении производных.
, который основан на применении производных.
Теорема 25.4 (Правило Лопиталя раскрытия неопределенностей вида 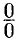 ). Пусть функции
). Пусть функции  и
и 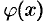 непрерывны и дифференцируемы в окрестности точки
непрерывны и дифференцируемы в окрестности точки  и обращаются в нуль в этой точке:
и обращаются в нуль в этой точке: 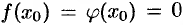 . Пусть
. Пусть 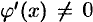 в окрестности точки
в окрестности точки  . Если существует предел
. Если существует предел 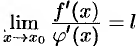 , то
, то 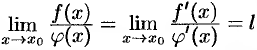 .
.
Применим к функциям  и
и 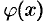 теорему Коши для отрезка
теорему Коши для отрезка 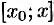 , лежащего в окрестности точки
, лежащего в окрестности точки  . Тогда
. Тогда 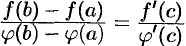 , где лежит между
, где лежит между  и
и  (рис. 144). Учитывая, что
(рис. 144). Учитывая, что 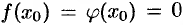 получаем
получаем

При  , величина
, величина 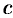 также стремится к
также стремится к  ; перейдем в равенстве (25.4) к пределу:
; перейдем в равенстве (25.4) к пределу:
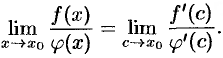
Так как 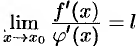 , то
, то 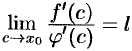 . Поэтому
. Поэтому 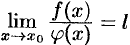 .
.
Коротко полученную формулу читают так: предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует.
Замечания: 1. Теорема 25.4 верна и в случае, когда функции  и
и 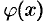 не определены при
не определены при 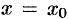 , но
, но 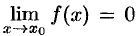 и
и 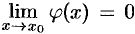 .
.
Достаточно положить 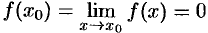 и
и 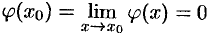 .
.
2. Теорема 25.4 справедлива и в том случае, когда 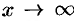 . Действительно, положив
. Действительно, положив 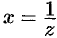 , получим
, получим
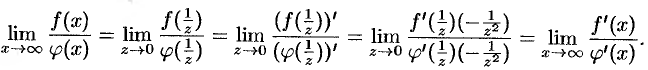
3. Если производные 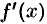 и
и 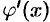 удовлетворяют тем же условиям, что и функции
удовлетворяют тем же условиям, что и функции  и
и 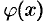 , теорему 25.4 можно применить еще раз:
, теорему 25.4 можно применить еще раз:
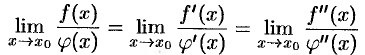
и т. д.
Пример №25.2.
Найти 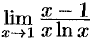 .
.
Решение:
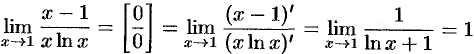 .
.
Дополнительный пример №25.3.
Теорема 25.4 дает возможность раскрывать неопределенность вида 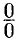 . Сформулируем без доказательства теорему о раскрытии неопределенности вида
. Сформулируем без доказательства теорему о раскрытии неопределенности вида 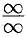 .
.
Теорема 25.5 (Правило Лопиталя раскрытия неопределенностей вида 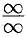 ).
).
Пусть функции  и
и 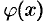 непрерывны и дифференцируемы в окрестности точки
непрерывны и дифференцируемы в окрестности точки  (кроме, может быть, точки
(кроме, может быть, точки  ), в этой окрестности
), в этой окрестности 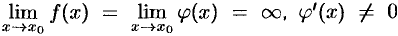 . Если существует предел
. Если существует предел 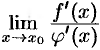 , то
, то 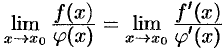 .
.
Пример №25.4.
Найти 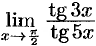 .
.
Решение:
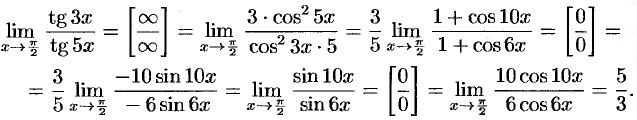
2-й способ:
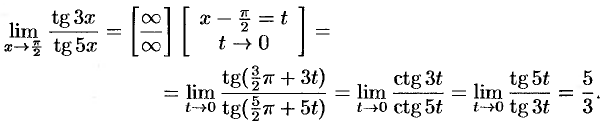
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Производная сложной и обратной функций |
| Гиперболические функции и их производные |
| Раскрытие неопределенностей различных видов |
| Формула Тейлора для функции |

