Связь между непрерывностью и дифференцируемостью функции
Теорема 20.1. Если функция дифференцируема в некоторой точке, то она непрерывна в ней.
Пусть функция  дифференцируема в некоторой точке
дифференцируема в некоторой точке  . Следовательно, существует предел
. Следовательно, существует предел 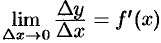 .
.
Отсюда, по теореме 17.5 о связи функции, ее предела и бесконечно малой функции, имеем 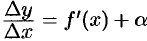 , где
, где 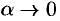 при
при 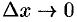 , то есть
, то есть 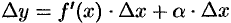 .
.
Переходя к пределу, при 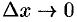 , получаем
, получаем 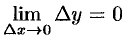 . А это и означает, что функция
. А это и означает, что функция  непрерывна в точке
непрерывна в точке  .
.
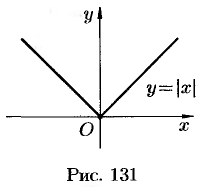
Обратная теорема неверна: непрерывная функция может не иметь производной. Примером такой функции является функция
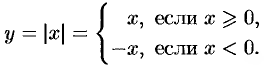
Изображенная на рисунке 131 функция непрерывна в точке 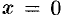 , но не дифференцируем в ней.
, но не дифференцируем в ней.
Действительно, в точке 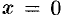 имеем
имеем
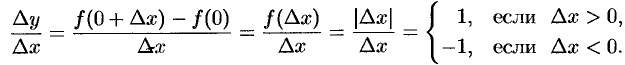
Отсюда следует, что 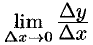 не существует, т. е. функция
не существует, т. е. функция 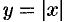 не имеет производной в точке
не имеет производной в точке 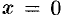 , график функции не имеет касательной в точке
, график функции не имеет касательной в точке 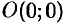 .
.
Замечания: 1. Существуют односторонние пределы функции 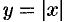 в точке
в точке 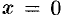 :
: 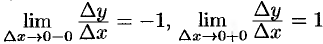 . В таких случаях говорят, что функция имеет односторонние производные (или «производные слева и справа»), и обозначают соответственно
. В таких случаях говорят, что функция имеет односторонние производные (или «производные слева и справа»), и обозначают соответственно 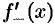 и
и 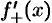 .
.
Если 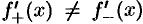 , то производная в точке не существует. Не существует производной и в точках разрыва функции.
, то производная в точке не существует. Не существует производной и в точках разрыва функции.
2. Производная 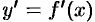 непрерывной функции
непрерывной функции  сама не обязательно является непрерывной.
сама не обязательно является непрерывной.
Если функция  имеет непрерывную производную
имеет непрерывную производную 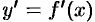 в некотором интервале
в некотором интервале 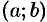 , то функция называется гладкой.
, то функция называется гладкой.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Скорость прямолинейного движения |
| Касательная к кривой |
| Производная суммы, разности, произведения и частного функций |
| Производная сложной и обратной функций |

