Скорость прямолинейного движения
Пусть материальная точка (некоторое тело)  движется неравномерно по некоторой прямой. Каждому значению времени
движется неравномерно по некоторой прямой. Каждому значению времени  соответствует определенное расстояние
соответствует определенное расстояние 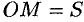 до некоторой фиксированной точки
до некоторой фиксированной точки 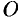 . Это расстояние зависит от истекшего времени
. Это расстояние зависит от истекшего времени  , т.е.
, т.е. 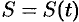 .
.
Это равенство называют законом движения точки. Требуется найти скорость движения точки.
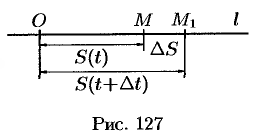
Если в некоторый момент времени  точка занимает положение
точка занимает положение  , то в момент времени
, то в момент времени 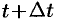 (
(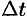 — приращение времени) точка займет положение
— приращение времени) точка займет положение 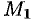 , где
, где 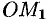
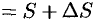 (
(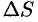 приращение расстояния (см. рис. 127). Таким образом, перемещение точки
приращение расстояния (см. рис. 127). Таким образом, перемещение точки  за время
за время 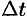 будет
будет 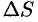
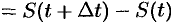 .
.
Отношение 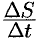 выражает среднюю скорость движения точки за время
выражает среднюю скорость движения точки за время 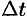 :
:
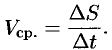
Средняя скорость зависит от значения 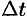 : чем меньше
: чем меньше 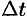 , тем точнее средняя скорость выражает скорость движения точки в данный момент времени
, тем точнее средняя скорость выражает скорость движения точки в данный момент времени  .
.
Предел средней скорости движения при стремлении к нулю промежутка времени 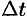 называется скоростью движения точки в данный момент времени (или мгновенной скоростью). Обозначив эту скорость через
называется скоростью движения точки в данный момент времени (или мгновенной скоростью). Обозначив эту скорость через 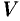 , получим
, получим
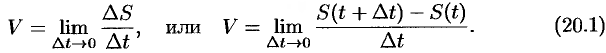
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Основные теоремы о непрерывных функциях |
| Свойства функций, непрерывных на отрезке |
| Касательная к кривой |
| Связь между непрерывностью и дифференцируемостью функции |

