Оглавление:
Свойства функций, непрерывных на отрезке
Непрерывные на отрезке функции имеют ряд важных свойств. Сформулируем их в виде теорем, не приводя доказательств.
Теорема 19.4 (Вейерштрасса). Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.
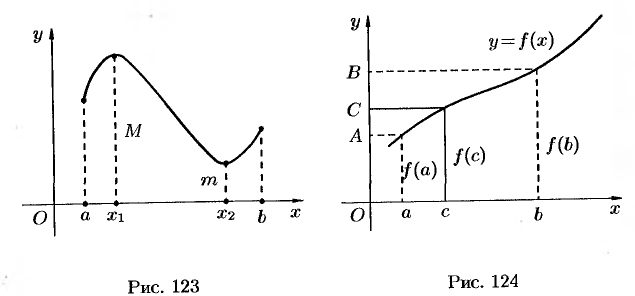
Изображенная на рисунке 123 функция  непрерывна на отрезке
непрерывна на отрезке  , принимает свое наибольшее значение
, принимает свое наибольшее значение  в точке
в точке 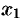 , а наименьшее
, а наименьшее 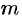 — в точке
— в точке 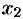 . Для любого
. Для любого 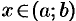 имеет место неравенство
имеет место неравенство 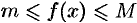 .
.
Следствие 19.1. Если функция непрерывна на отрезке, то она ограничена на этом отрезке.
Теорема 19.5 (Больцано-Коши). Если функция  непрерывна на отрезке
непрерывна на отрезке  и принимает на его концах неравные значения
и принимает на его концах неравные значения 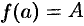 и
и 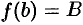 , то на этом отрезке она принимает и все промежуточные значения между
, то на этом отрезке она принимает и все промежуточные значения между  и
и 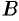 .
.
Геометрически теорема очевидна (см. рис. 124).
Для любого числа 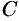 , заключенного между
, заключенного между  и
и 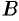 , найдется точка
, найдется точка 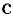 внутри этого отрезка такая, что
внутри этого отрезка такая, что 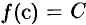 . Прямая
. Прямая 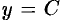 пересечен график функции по крайней мере в одной точке.
пересечен график функции по крайней мере в одной точке.
Следствие 19.2. Если функция  непрерывна на отрезке
непрерывна на отрезке  и на его концах принимает значения разных знаков, то внутри отрезка
и на его концах принимает значения разных знаков, то внутри отрезка  найдется хотя бы одна точка
найдется хотя бы одна точка 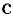 , в которой данная функция
, в которой данная функция  обращается в нуль:
обращается в нуль: 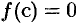 .
.
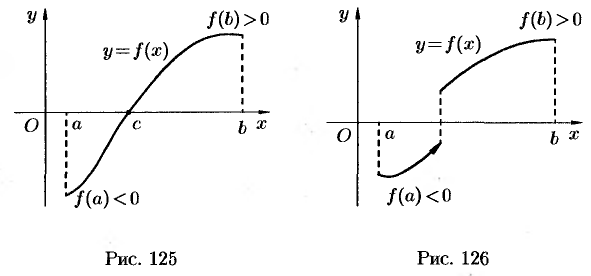
Геометрический смысл теоремы: если график непрерывной функции переходит с одной стороны оси  на другую, то он пересекает оси
на другую, то он пересекает оси  (см. рис. 125).
(см. рис. 125).
Следствие 19.2 лежит в основе так называемого «метода половинного деления», который используется для нахождения корня уравнения 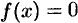 .
.
Утверждения теорем 19.4 и 19.5, вообще говоря, делаются неверными, если нарушены какие-либо из ее условий: функция непрерывна не на отрезке  , а в интервале
, а в интервале 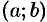 , либо функция на отрезке
, либо функция на отрезке  имеет разрыв.
имеет разрыв.
Рисунок 126 показывает это для следствия теоремы 19.5: график разрывной функции не пересекает ось  .
.
Пример №19.5.
Определить с точностью до 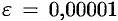 корень уравнения
корень уравнения 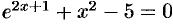 , принадлежащий отрезку [0; 1], применив метод половинного деления.
, принадлежащий отрезку [0; 1], применив метод половинного деления.
Решение:
Обозначим левую часть уравнения через  .
.
Шаг 1. Вычисляем 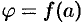 и
и 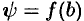 , где
, где 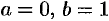 .
.
Шаг 2. Вычисляем 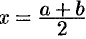 .
.
Шаг 3. Вычисляем  . Если
. Если 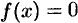 , то
, то  — корень уравнения.
— корень уравнения.
Шаг 4. При 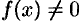 если
если 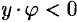 , то полагаем
, то полагаем 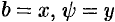 , иначе полагаем
, иначе полагаем 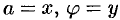 .
.
Шаг 5. Если  , то задача решена. В качестве искомого корня (с заданной точностью
, то задача решена. В качестве искомого корня (с заданной точностью 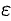 ) принимается величина
) принимается величина 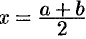 . Иначе процесс деления отрезка
. Иначе процесс деления отрезка  пополам продолжаем, возвращаясь к шагу 2.
пополам продолжаем, возвращаясь к шагу 2.
В результате произведенных действий получим: 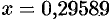 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Точки разрыва функции и их классификация |
| Основные теоремы о непрерывных функциях |
| Скорость прямолинейного движения |
| Касательная к кривой |

