Числовые промежутки. Окрестность точки
Пусть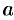 
и 
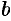— действительные числа, причем 
.
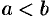Числовыми промежутками (интервалами) называют подмножества всех действительных чисел, имеющих следующий вид:
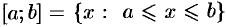— отрезок (сегмент, замкнутый промежуток);
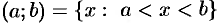— интервал (открытый промежуток);
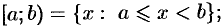
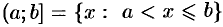— полуоткрытые интервалы (или полуоткрытые отрезки);
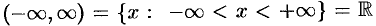— бесконечные интервалы (промежутки).
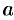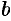Числа и называются соответственно левым и правым концами этих промежутков. Символы 
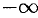и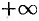 
не числа, это символическое обозначение процесса неограниченного удаления точек числовой оси означала 0 влево и вправо.
Пусть 
— любое действительное число (точка на числовой прямой). Окрестностью точки хо называется любой интервал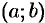 
, содержащий точку . В частности, интервал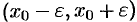 
, где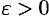 
, называется 
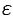-окрестностью точки . Число называется центром, а число 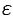— радиусом.
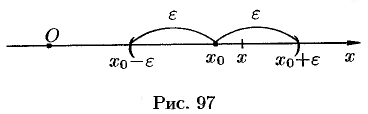
Если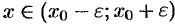 
, то выполняется неравенство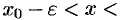 
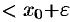, или, что то же, 
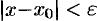. Выполнение последнего неравенства означает попадание точки 
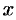в 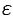-окрестность точки (см. рис. 97).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Множество действительных чисел |
| Числовые множества |
| Предельный переход в неравенствах |
| Предел монотонной ограниченной последовательности |
