Оглавление:
Поверхности вращения. Конические поверхности
Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости, называется поверхностью вращения. Пусть некоторая кривая 
лежит в плоскости 
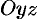. Уравнения этой кривой запишутся в виде
Найдем уравнение поверхности, образованной вращением кривой вокруг оси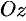 
.
Возьмем на поверхности произвольную точку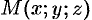 
(см. рис. 88). Проведем через точку 
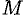плоскость, перпендикулярную оси 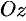, и обозначим точки пересечения ее с осью 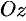и кривой соответственно через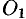 
и 
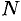. Обозначим координаты точки 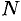через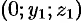 
. Отрезк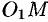и 
и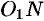 
являются радиусами одной и той же окружности. Поэтому 
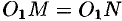. Но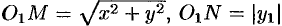 
. Следовательно, 
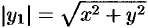или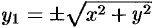 
. Кроме того, очевидно, 
.
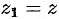Так как точка 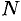лежит на кривой , то ее координаты удовлетворяют уравнению (12.22). Стало быть,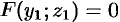 
. Исключая вспомогательные координаты 
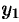и 
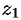точки 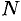, приходим к уравнению
Уравнение (12.23) — искомое уравнение поверхности вращения, ему удовлетворяют координаты любой точки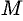 
этой поверхности и не удовлетворяют координаты точек, не лежащих на поверхности вращения.
Как видно, уравнение (12.23) получается из (12.22) простой заменой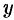 
на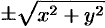 
, координата 
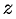сохраняется.
Понятно, что если кривая (12.22) вращается вокруг оси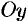 
, то уравнение поверхности вращения имеет вид
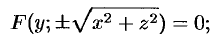
если кривая лежит в плоскости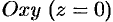 
и ее уравнение 
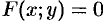, то уравнение поверхности вращения, образованной вращением кривой вокруг оси 
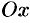, есть 
.
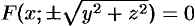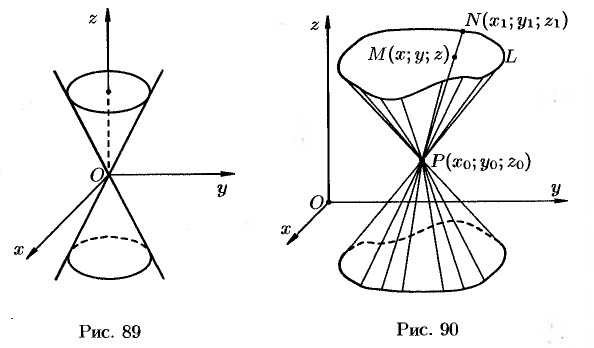
Так, например, вращая прямую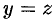 
вокруг оси 
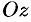(см. рис. 89), получим поверхность вращения (ее уравнение 
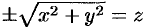или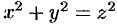 
). Она называется конусом второго порядка.
Поверхность, образованная прямыми линиями, проходящими через данную точку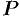 
и пересекающими данную плоскую линию 
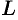(не проходящую через 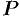), называется конической поверхностью или конусом. При этом линия 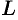называется направляющей конуса, точка 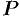— ее вершиной, а прямая, описывающая поверхность, называется образующей.
Пусть направляющая 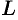задана уравнениями
а точка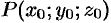 
— вершина конуса. Найдем уравнение конуса.
Возьмем на поверхности конуса произвольную точку 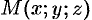(см. рис. 90). Образующая, проходящая через точк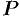и и 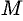, пересечет направляющую 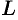в некоторой точке 
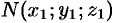. Координаты точки 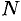удовлетворяют уравнениям (12.24) направляющей:
Канонические уравнения образующих, проходящих через точк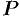и и 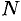, имеют вид
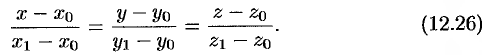
Исключая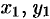 
и 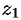из уравнений (12.25) и (12.26), получим уравнение конической поверхности, связывающее текущие координаты 
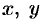и .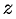
Пример №12.3.
Составить уравнение конуса с вершиной в точке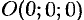 
, если направляющей служит эллипс 
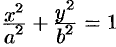, лежащий в плоскости 
.
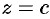Решение:
Пусть 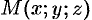— любая точка конуса. Канонические уравнения образующих, проходящих через точки (0; 0; 0) и точку 
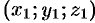пересечения образующей 
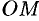с эллипсом будут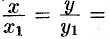 
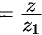. Исключим 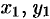и 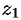из этих уравнений и уравнения
(точка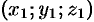 
лежит на эллипсе), 
. Имеем: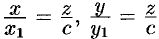 
. Отсюда 
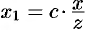и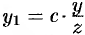 
. Подставляя значения 
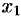и 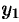в уравнение эллипса (12.27), получим
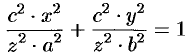или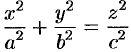 
.
Это и есть искомое уравнение конуса.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Прямая и плоскость в пространстве |
| Цилиндрические поверхности |
| Множество действительных чисел |
| Числовые множества |
