Оглавление:
Некоторые приложения скалярного произведения
Угол между векторами
Определение угла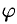 
между ненулевыми векторами 
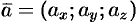и 
:
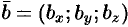т. е. 
Отсюда следует условие перпендикулярности ненулевых векторов 
и 
:
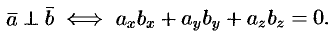
Проекция вектора на заданное направление
Нахождение проекции вектора на направление, заданное вектором , может осуществляться по формуле
т.е. 
Работа постоянной силы
Пусть материальная точка перемещается прямолинейно из положения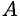 
в положение 
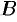под действием постоянной силы 
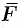, образующей угол 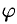с перемещением 
(см. рис. 15).
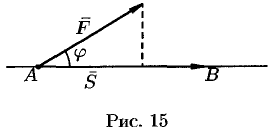
Из физики известно, что работа силы 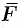при перемещении 
равна 
, т. е. 
.
Таким образом, работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.
Пример №6.3.
Вычислить работу, произведенную силой 
, если точка ее приложения перемещается прямолинейно из положения 
в положение 
. Под каким углом к 
направлена сила ?
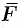Решение:
Находим 
. Стало быть, 
(ед. работы).
Угол 
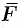между и находим по формуле
, т. е.
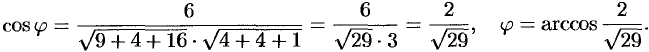
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Скалярное произведение векторов и его свойства |
| Выражение скалярного произведения через координаты |
| Векторное произведение векторов и его свойства |
| Смешанное произведение векторов |
