Оглавление:
Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
Рассмотрим в пространстве прямоугольную систему координат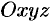 
. Выделим на координатных осях 
, 
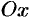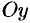и 
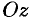единичные векторы (орты), обозначаемые 
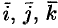соответственно (см. рис. 12).
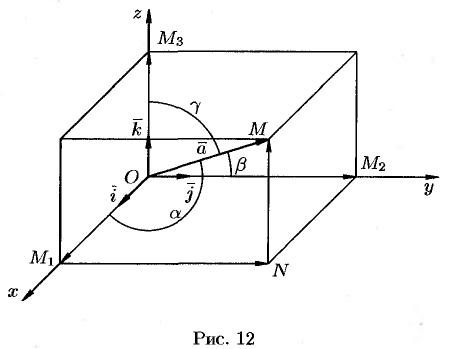
Выберем произвольный вектор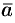 
пространства и совместим его начало с началом координат: 
.
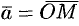Найдем проекции вектора 
на координатные оси. Проведем через конец вектора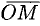 
плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через 
, 
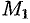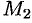и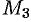 
. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор 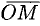. Тогда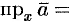 
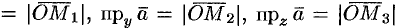. По определению суммы нескольких векторов находим 
.
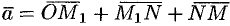А так как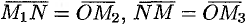 
, то
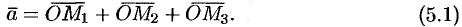
Но
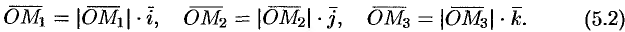
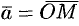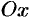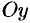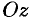Обозначим проекции вектора на оси , и соответственно через 
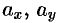и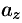 
, т. е. 
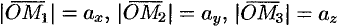. Тогда из равенств (5.1) и (5.2) получаем
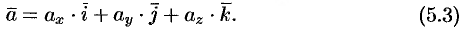
Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных oсей.
Числа 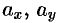, 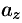называются координатами вектора , т. е. координаты вектора есть его проекции на соответствующие координатные оси.
Векторное равенство (5.3) часто записывают в символическом виде: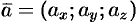 
.
Равенство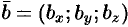 
означает, что 
.
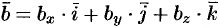Зная проекции вектора 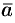, можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать 
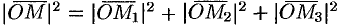, т. е.
Отсюда
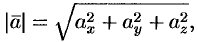
т. е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
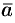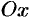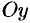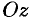Пусть углы вектора с осями , и соответственно равны 
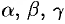. По свойству проекции вектора на ось, имеем
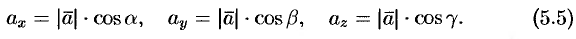
Или, что то же самое,
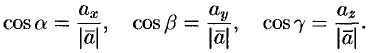
Числа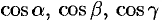 
называются направляющими косинусами вектора .
Подставим выражения (5.5) в равенство (5.4), получаем
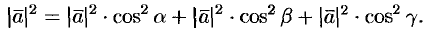
Сократив на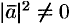 
, получим соотношение
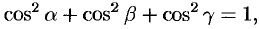
т. е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.
Легко заметить, что координатами единичного вектора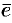 
являются числа 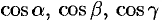, т. е. 
.
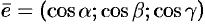Итак, задав координаты вектора, всегда можно определить его модуль и направление, т. е. сам вектор.
Действия над векторами, заданными проекциями
Пусть векторы 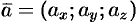и 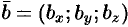заданы своими проекциями на оси координат 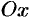, , 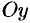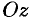или, что то же самое
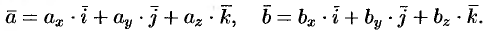
Линейные операции над векторами
Так как линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можно записать:
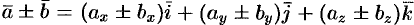, или кратко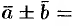 
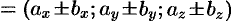. То есть при сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).
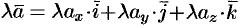или короче 
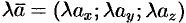. То есть при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.
Равенство векторов
Из определения вектора как направленного отрезка, который можно передвигать в пространстве параллельно самому себе, следует, что два вектора 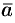и 
равны тогда и только тогда, когда выполняются равенства: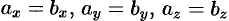 
, т. е.
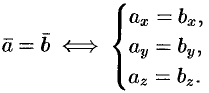
Коллинеарность векторов
Выясним условия коллинеарности векторов и , заданных своими координатами.
Так как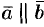 
, то можно записать 
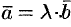, где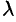 
— некоторое число. То есть
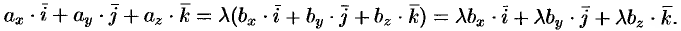
Отсюда
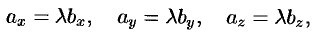
т.е.
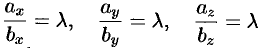или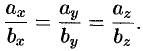 
Таким образом, проекции коллинеарных векторов пропорциональны. Верно и обратное утверждение: векторы, имеющие пропорциональные координаты, коллинеарны.
Координаты точки
Пусть в пространстве задана прямоугольная декартова система координат 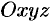. Для любой точки 
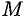координаты вектора 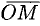называются координатами точки 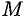. Вектор 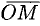называется радиус-вектором точки 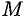, обозначается 
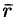, т. е. 
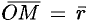. Следовательно, координаты точки — это координаты ее радиус-вектора
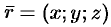или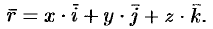 
Координаты точки 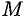записываются в виде 
.
Координаты вектора
Найдем координаты вектора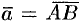 
, если известны координаты точек 
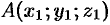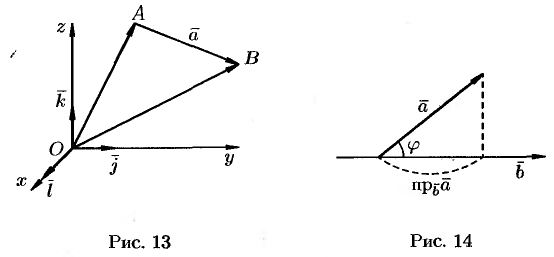
и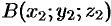 
. Имеем (см. рис. 13):
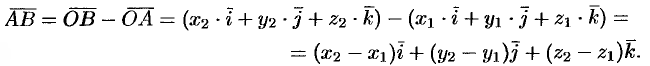
Следовательно, координаты вектора равны разностям соответствующих координат его конца и начала: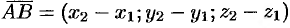 
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Линейные операции над векторами |
| Проекция вектора на ось |
| Скалярное произведение векторов и его свойства |
| Выражение скалярного произведения через координаты |
