Проекция вектора на ось
Пусть в пространстве задана ось 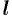 , т. е. направленная прямая.
, т. е. направленная прямая.
Проекцией точки 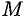 на ось
на ось 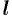 называется основание
называется основание 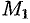 перпендикуляра
перпендикуляра 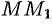 , опущенного из точки на ось.
, опущенного из точки на ось.
Точка есть точка пересечения оси 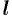 с плоскостью, проходящей через точку
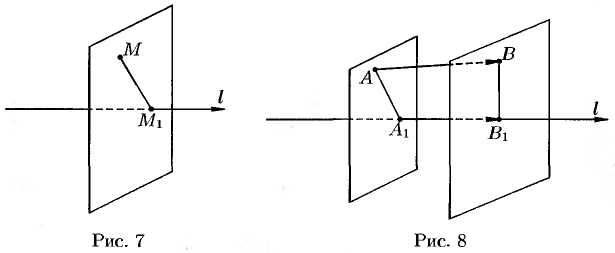
с плоскостью, проходящей через точку 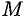 перпендикулярно оси (см. рис. 7).
перпендикулярно оси (см. рис. 7).
Если точка 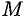 лежит на оси
лежит на оси 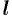 , то проекция точки
, то проекция точки 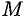 на ось совпадает с
на ось совпадает с 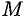 .
.
Пусть 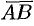 — произвольный вектор (
— произвольный вектор (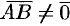 ). Обозначим через
). Обозначим через 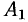 и
и 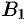 проекции на ось
проекции на ось 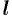 соответственно начала
соответственно начала 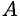 и конца
и конца 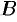 вектора
вектора 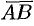 и рассмотрим вектор
и рассмотрим вектор 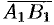 .
.
Проекцией вектора 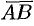 на ось
на ось 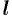 называется положительное число
называется положительное число 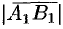 , если вектор
, если вектор 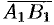 и ось
и ось 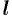 одинаково направлены и отрицательное число —
одинаково направлены и отрицательное число — 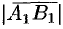 , если вектор
, если вектор 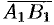 и ось
и ось 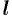 противоположно направлены (см. рис. 8). Если точки
противоположно направлены (см. рис. 8). Если точки 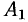 и
и 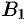 совпадают (
совпадают (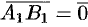 ), то проекция вектора
), то проекция вектора 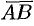 равна 0.
равна 0.
Проекция вектора 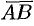 на ось
на ось 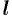 обозначается так:
обозначается так: 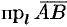 . Если
. Если 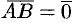 или
или 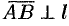 , то
, то 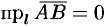 .
.
Угол 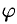 между вектором
между вектором  и осью
и осью 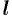 (или угол между двумя векторами) изображен на рисунке 9. Очевидно,
(или угол между двумя векторами) изображен на рисунке 9. Очевидно, 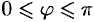 .
.
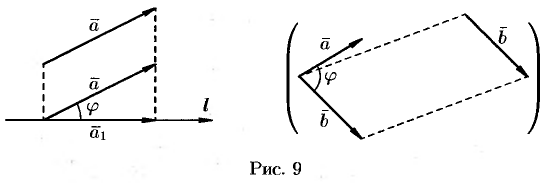
Рассмотрим некоторые основные свойства проекций.
Свойство 1. Проекция вектора 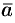 на ось
на ось 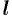 равна произведению модуля вектора
равна произведению модуля вектора 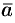 на косинус угла
на косинус угла 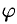 между вектором и осью, т. е.
между вектором и осью, т. е. 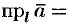
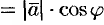 .
.
Если 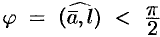 , то
, то 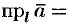
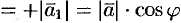 .
.
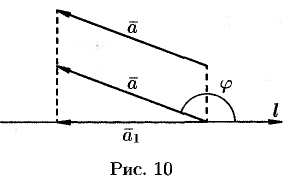
Если 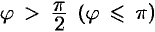 , то
, то 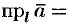
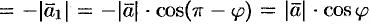 (см. рис. 10).
(см. рис. 10).
Если 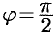 , то
, то 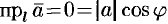 .
.
Следствие 5.1. Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол — прямой.
Следствие 5.2. Проекции равных векторов на одну и ту же ось равны между собой.
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.
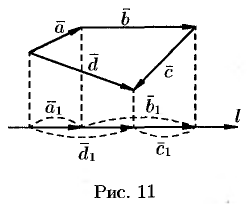
Пусть, например, 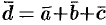 . Имеем
. Имеем 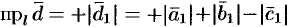 , т. е.
, т. е. 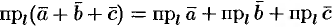 (см. рис. 11).
(см. рис. 11).
Свойство 3. При умножении вектора 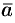 на число
на число 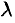 его проекция на ось также умножается на это число, т. е.
его проекция на ось также умножается на это число, т. е.
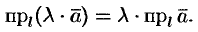
При 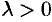 имеем
имеем
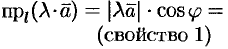
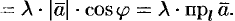
При 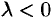 :
: 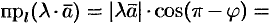
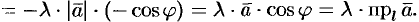 Свойство справедливо, очевидно, и при
Свойство справедливо, очевидно, и при 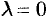 .
.
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Системы линейных однородных уравнений |
| Линейные операции над векторами |
| Разложение вектора по ортам координатных осей |
| Скалярное произведение векторов и его свойства |

