Линейные операции над векторами
Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
Пусть 
и 
— два произвольных вектора. Возьмем произвольную точку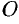 
и построим вектор 
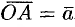. От точки 
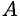отложим вектор 
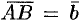. Вектор 
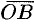, соединяющий начало первого вектора с концом второго, называется суммой векторов и : 
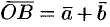(см. рис. 2).
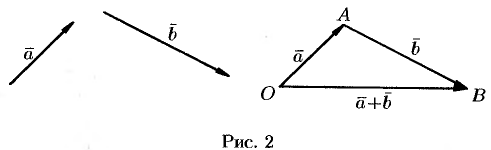
Это правило сложения векторов называют правилом треугольника.
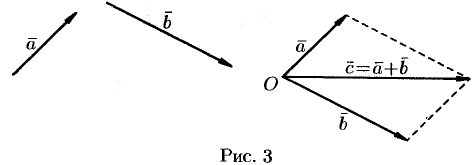
Сумму двух векторов можно построить также по правилу параллелограмма (см. рис. 3).
На рисунке 4 показано сложение трех векторов , и 
.
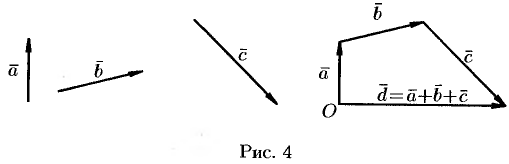
Под разностью векторов и понимается вектор 
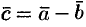такой, что 
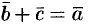(см. рис. 5).
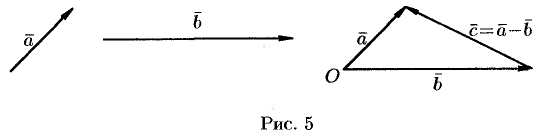
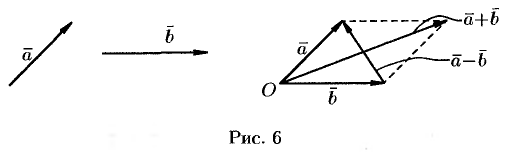
Отметим, что в параллелограмме, построенном на векторах и , одна направленная диагональ является суммой векторов и , а другая — разностью (см. рис. 6).
Можно вычитать векторы по правилу: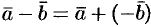 
, т. е. вычитание векторов заменить сложением вектора с вектором, противоположным вектору .
Произведением вектора а на скаляр (число)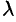 
называется вектор 
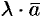(или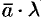 
), который имеет длину 
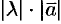, коллинеарен вектору , имеет направление вектора , если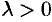 
и противоположное направление, если 
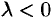. Например, если дан вектор 
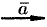, то векторы 
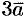и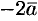 
будут иметь вид 
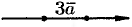и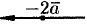 
.
Из определения произведения вектора на число следуют свойства этого произведения:
1) если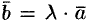 
, то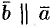 
. Наоборот, если , 
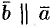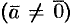, то при некотором 
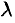верно равенство 
;
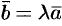2) всегда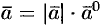 
, т. е. каждый вектор равен произведению его модуля на орт.
Линейные операции над векторами обладают следующими свойствами:
Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Элементарные преобразования матриц |
| Системы линейных однородных уравнений |
| Проекция вектора на ось |
| Разложение вектора по ортам координатных осей |
