Нули аналитической функции
Как показано выше, всякая функция 
, аналитическая в окрестности точки 
, разлагается в этой окрестности в степенной ряд (76.7): коэффициенты которого определяются по формулам (76.8).
Точка называется нулем функции , если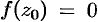 
. В этом случае разложение функции в окрестности точки в степенной ряд не содержит нулевого члена, т. к.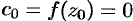 
. Если не только 
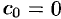, но и 
, a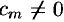 
, то разложение функции в окрестности точки имеет вид
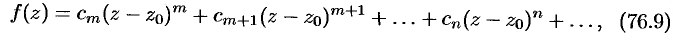
а точка называется нулем кратности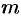 
(или нулем 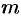-го порядка). Если 
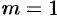, то называется простым нулем.
Из формул (76.8) для коэффициентов ряда Тейлора следует, что если является нулем кратности 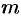функции , то 
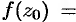
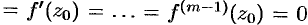, но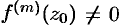 
. В этом случае представление функции степенным рядом (76.9) можно переписать в ви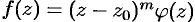де 
, где
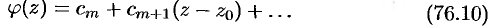
Для функции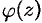 
точка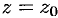 
уже не является нулем, так как 
.
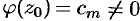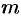Справедливо и обратное утверждение: если функция имеет вид (76.10), где — натуральное число, а 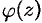аналитична в точке , причем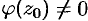 
, то точка есть нуль кратности 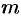функции .
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Интегральная теорема Коши |
| Интеграл Коши. Интегральная формула Коши |
| Классификация особых точек. Связь между нулем и полюсом функции |
| Устранимые особые точки |
