Оглавление:
Аналитическая функция. Дифференциал
Фундаментальным понятием в теории функций комплексного переменного является понятие аналитической функции.
Однозначная функция  называется аналитической (голоморфной) в точке
называется аналитической (голоморфной) в точке  , если она дифференцируема (выполнены условия Эйлера-Даламбера) в некоторой окрестности этой точки. Функция
, если она дифференцируема (выполнены условия Эйлера-Даламбера) в некоторой окрестности этой точки. Функция  называется аналитической в области
называется аналитической в области  , если она дифференцируема в каждой точке
, если она дифференцируема в каждой точке 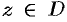 .
.
Как видно из этого определения, условие аналитичности в точке не совпадает с условием дифференцируемости функции в этой же точке (первое условие — более сильное).
Точки плоскости  , в которых однозначная функция
, в которых однозначная функция  аналитична, называются правильными точками
аналитична, называются правильными точками  . Точки, в которых функция
. Точки, в которых функция  не является аналитической, называются особыми точками этой функции.
не является аналитической, называются особыми точками этой функции.
Пусть функция  аналитична в точке
аналитична в точке  . Тогда
. Тогда 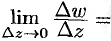
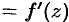 . Отсюда следует, что
. Отсюда следует, что 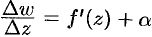 , где
, где 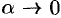 при
при 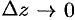 . Тогда приращение функции можно записать так:
. Тогда приращение функции можно записать так: 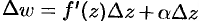 . Если
. Если 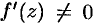 , то первое слагаемое
, то первое слагаемое 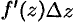 является при
является при 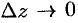 бесконечно малой того же порядка, что и
бесконечно малой того же порядка, что и 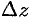 ; второе слагаемое
; второе слагаемое 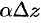 ; есть бесконечно малая более высокого порядка, чем
; есть бесконечно малая более высокого порядка, чем 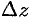 . Следовательно, первое слагаемое составляет главную часть приращения функции
. Следовательно, первое слагаемое составляет главную часть приращения функции  .
.
Дифференциалом 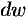 аналитической функции
аналитической функции  в точке
в точке  называется главная часть ее приращения, т. е.
называется главная часть ее приращения, т. е. 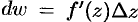 , или
, или 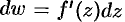 (так как при
(так как при 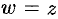 будет
будет 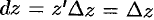 ). Отсюда следует, что
). Отсюда следует, что 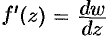 , т. е. производная функции равна отношению дифференциала функции к дифференциалу независимого переменного.
, т. е. производная функции равна отношению дифференциала функции к дифференциалу независимого переменного.
Замечание. Если функция 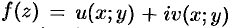 аналитична в некоторой области
аналитична в некоторой области  , то функции
, то функции 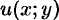 и
и 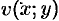 удовлетворяют дифференциальному уравнению Лапласа (
удовлетворяют дифференциальному уравнению Лапласа (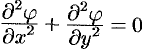 , см. п. 72.2).
, см. п. 72.2).
Действительно, дифференцируя первое из равенств Эйлера-Даламбера по  , а второе по
, а второе по  , получаем:
, получаем:
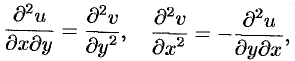
откуда 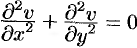 .
.
Функции 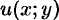 и
и 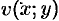 являются гармоническими функциями.
являются гармоническими функциями.
Пример №74.3.
Проверить, является ли функция 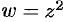 аналитической. Найти ее производную.
аналитической. Найти ее производную.
Решение:
Находим действительную 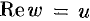 и мнимую
и мнимую 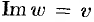 части функции:
части функции:
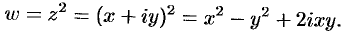
Таким образом, 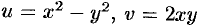 . Проверяем условия Эйлера-Даламбера (74.5):
. Проверяем условия Эйлера-Даламбера (74.5):
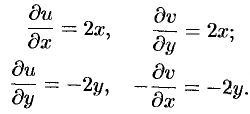
Условия (74.5) выполняются во всех точках комплексной плоскости  . Функция
. Функция 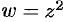 дифференцируема, следовательно, аналитична во всех точках этой плоскости. Ее производную найдем по одной из формул (74.6), например по первой:
дифференцируема, следовательно, аналитична во всех точках этой плоскости. Ее производную найдем по одной из формул (74.6), например по первой:
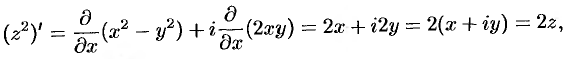
т. е. 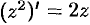 .
.
Заметим, что производную функции 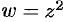 можно найти, воспользовавшись определением производной (74.4):
можно найти, воспользовавшись определением производной (74.4):
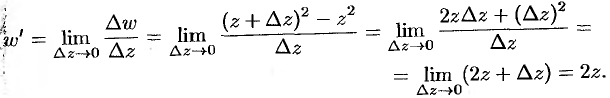
Пример №74.4.
Найти аналитическую функцию 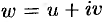 по ее заданной действительной части
по ее заданной действительной части 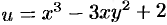 .
.
Решение:
Отметим, что функция и является гармонической функцией (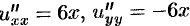 , следовательно,
, следовательно, 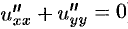 ).
).
Для определения мнимой части 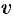 воспользуемся условиями Эйлера-Даламбера (74.5). Так как
воспользуемся условиями Эйлера-Даламбера (74.5). Так как 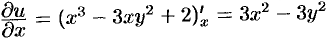 ,
,
то, согласно первому условию, 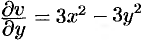 . Отсюда, интегрируя по
. Отсюда, интегрируя по  , находим:
, находим:
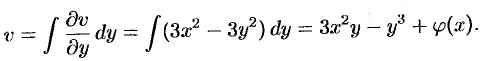
Для определения функции 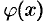 воспользуемся вторым условием Эйлера Даламбера. Так как
воспользуемся вторым условием Эйлера Даламбера. Так как
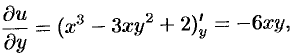
а
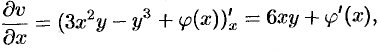
то 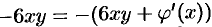 . Отсюда
. Отсюда 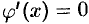 и
и 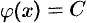 , где
, где 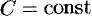 . Поэтому
. Поэтому 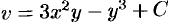 . Находим функцию
. Находим функцию 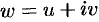 :
:
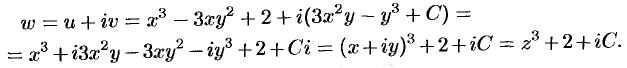
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Свойства основных классов векторных полей |
| Дифференцирование функции комплексного переменного |
| Геометрический смысл модуля и аргумента производной |
| Интегрирование функции комплексного переменного |

