Ротор поля. Формула Стокса
Ротором (или вихрем) векторного поля
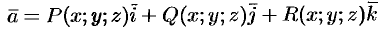
называется вектор, обозначаемый 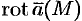 и определяемый формулой
и определяемый формулой
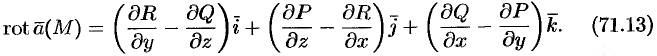
Формулу (71.13) можно записать с помощью символического определителя в виде, удобном для запоминания:
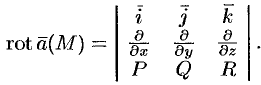
Отметим некоторые свойства ротора.
- Если
 — постоянный вектор, то
— постоянный вектор, то 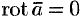 .
. 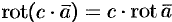 , где
, где 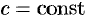 .
.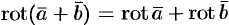 , т. e. ротор суммы двух векторов равен сумме роторов слагаемых.
, т. e. ротор суммы двух векторов равен сумме роторов слагаемых.- Если
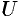 — скалярная функция, а
— скалярная функция, а 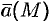 — векторная, то
— векторная, то
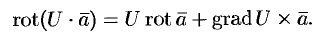
Эти свойства легко проверить, используя формулу (71.13). Покажем, например, справедливость свойства 3:
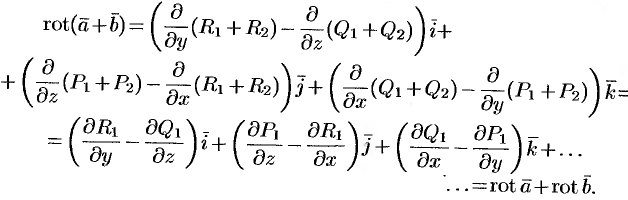
Используя понятия ротора и циркуляции, векторного поля, запишем известную в математическом анализе (см. п. 58.4) формулу Стокса:
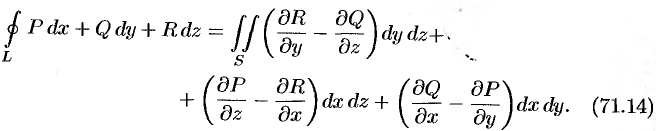
Левая часть формулы (71.14) представляет собой циркуляцию вектора  по контуру
по контуру  , т. е.
, т. е. 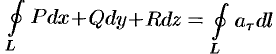 (см. (71.11)). Интеграл в правой части формулы (71.14) представляет собой поток вектора
(см. (71.11)). Интеграл в правой части формулы (71.14) представляет собой поток вектора 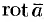 через поверхность
через поверхность  , ограниченную контуром
, ограниченную контуром  (см. (71.3)), т. е.
(см. (71.3)), т. е.
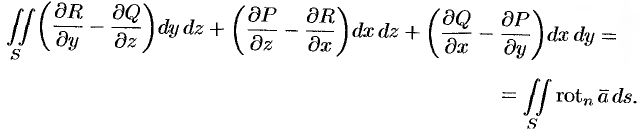
Следовательно, формулу Стокса можно записать в виде
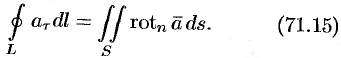
Такое представление формулы Стокса называют ее векторной формой. В этой формуле положительное направление на контуре  и выбор стороны у поверхности
и выбор стороны у поверхности  согласованы между собой так же, как в теореме Стокса.
согласованы между собой так же, как в теореме Стокса.
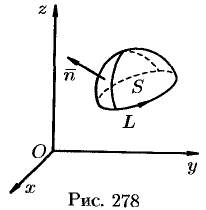
Формула (71.15) показывает, что циркуляция вектора  вдоль замкнутого контура
вдоль замкнутого контура  равна потоку ротора этого вектора
равна потоку ротора этого вектора  через поверхность
через поверхность  , лежащую в поле вектора
, лежащую в поле вектора  и ограниченную контуром
и ограниченную контуром  (натянутую на контур) (см. рис. 278).
(натянутую на контур) (см. рис. 278).
Используя формулу (71.14), можно дать другое определение ротора поля, эквивалентное первому и не зависящее от выбора координатной системы.
Для этого применим формулу Стокса (71.15) для достаточно малой плоской площадки  с контуром
с контуром  , содержащей точку
, содержащей точку  .
.
По теореме о среднем для поверхностного интеграла (п. 57.1, свойство 7) имеем:
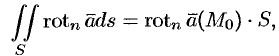
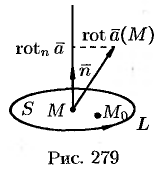
где 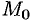 — некоторая (средняя) точка площадки
— некоторая (средняя) точка площадки  (см. рис. 279).
(см. рис. 279).
Тогда формулу (71.15) можно записать в виде
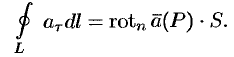
Отсюда:
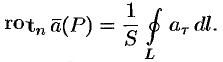
Пусть контур  стягивается в точку
стягивается в точку  . Тогда
. Тогда 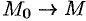 , a
, a 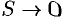 . Перейдя к пределу, получаем:
. Перейдя к пределу, получаем:
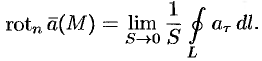
Ротором вектора  в точке
в точке  называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции вектора
называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции вектора  по контуру
по контуру  плоской площадки
плоской площадки  , перпендикулярной этому направлению, к площади этой площадки.
, перпендикулярной этому направлению, к площади этой площадки.
Как видно из определения, ротор вектора 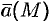 есть векторная величина, образующая собственное векторное поле.
есть векторная величина, образующая собственное векторное поле.
Дадим физическое истолкование понятия ротора векторного поля. Найдем ротор ноля линейных скоростей твердого тела, вращающегося вокруг оси 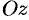 с постоянной угловой скоростью (пример 69.2)
с постоянной угловой скоростью (пример 69.2) 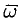 , т. е. ротор вектора
, т. е. ротор вектора 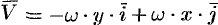 .
.
По определению ротора
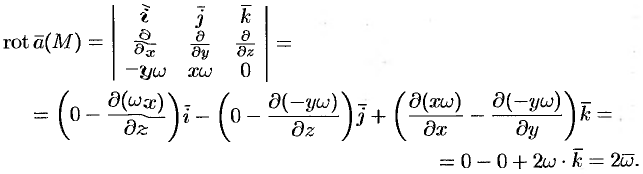
Ротор этого поля направлен параллельно оси вращения, его модуль равен удвоенной угловой скорости вращения.
С точностью до числового множителя ротор поля скоростей 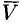 представляет собой угловую скорость вращения твердого тела. С этим связано само название «ротор» (лат. «вращатель»).
представляет собой угловую скорость вращения твердого тела. С этим связано само название «ротор» (лат. «вращатель»).
Замечание. Из определения (71.13) ротора вытекает, что направление ротора — это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадке  .
.
Так что связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению (см. п. 70.3).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Дивергенция поля. Формула Остроградского-Гаусса |
| Циркуляция векторного поля |
| Свойства основных классов векторных полей |
| Дифференцирование функции комплексного переменного |

