Оглавление:
Комплексная форма ряда Фурье
Ряды Фурье часто применяются в комплексной форме записи. Преобразуем ряд (66.12) и его коэффициенты (66.13) — (66.15) к комплексной форме. Для этого используем формулы Эйлера, выражающие косинус и синус, через показательную функцию:
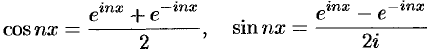
(из формулы Эйлера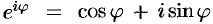 
и вытекающего из нее равенства 
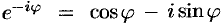находим, что 
, 
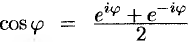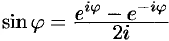). Подставив эти выражения в ряд (66.12), находим:
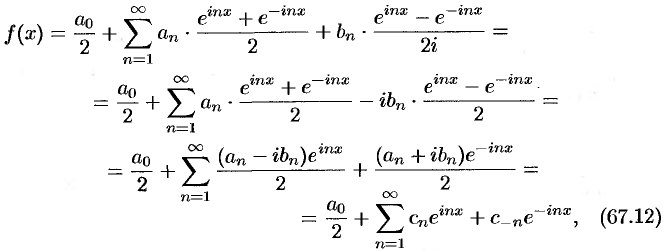
где обозначено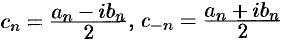 
.
Найдем выражения для комплексных коэффициентов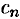 
и 
. И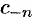спользуя выражения для 
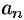и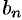 
(формулы (66.14) и (66.15)), получим:
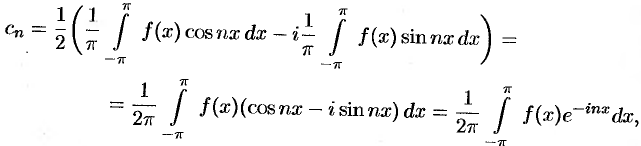
т. е.
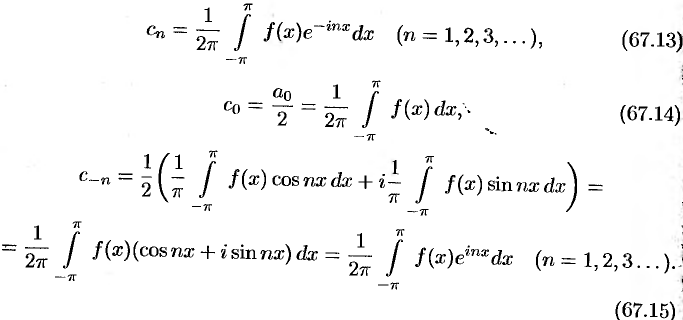
Таким образом, формулу (67.12) можно записать в виде
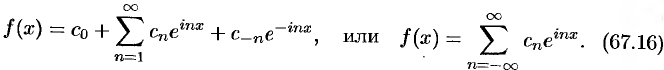
Коэффициенты этого ряда, согласно формулам (67.13) — (67.15), можно записать в виде
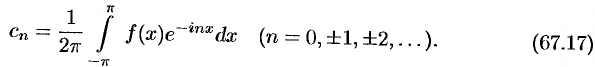
Равенство (67.16) называется комплексной формой ряда Фурье функции 
, а числа 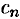, найденные по формуле (67.17), — комплексными коэффициентами ряда Фурье.
Если функция задается на отрезке 
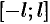, то комплексная форма ее ряда Фурье имеет вид
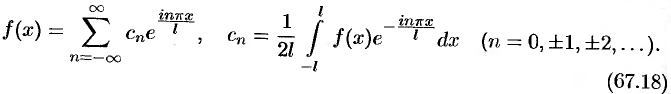
Как видим, комплексная форма ряда Фурье (и коэффициентов) более компактна, чем обыкновенный ряд Фурье.
В электротехнике и радиотехнике члены ряда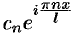 
называются гармониками, коэффициенты 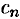— комплексными амплитудами гармоник, а числа 
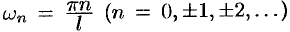— волновыми числами функции 
.
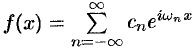Совокупность величин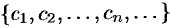 
называется амплитудным спектром.
Графически амплитудный спектр изображается в виде вертикальных отрезков длиной 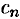, расположенных в точках 
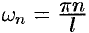числовой оси.
Пример №67.5.
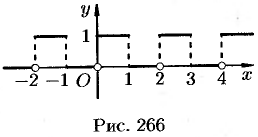
Построить ряд Фурье в комплексной форме для 2-периодической функции
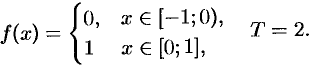
Решение:
На рисунке 266 изображен график функции . По формулам (67.18) находим (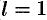
):
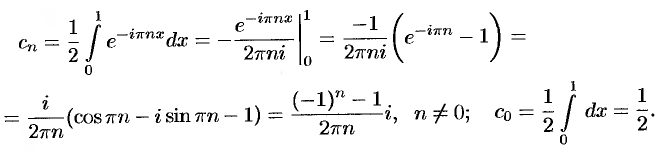
Следовательно, для всех точек непрерывности функции справедливо равенство
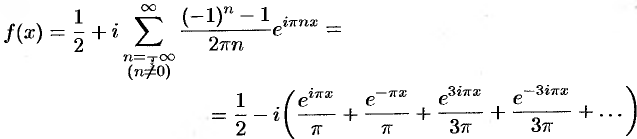
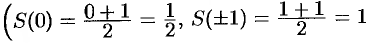на графике 
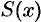не отмечена 
.
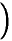На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Разложение в ряд Фурье функций произвольного периода |
| Представление непериодической функции рядом Фурье |
| Интеграл Фурье |
| Градиент скалярного поля и его свойства |
