Оглавление:
Приближенное вычисление определенных интегралов
Бесконечные ряды применяются также для приближенного вычисления неопределенных и определенных интегралов в случаях, когда первообразная не выражается в конечном виде через элементарные функции (см. § 34) либо нахождение первообразной сложно.
Пусть требуется вычислить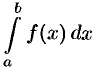 
с точностью до 
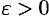. Если подынтегральную функцию 
можно разложить в ряд по степеням 
и интервал сходимости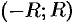 
включит в себя отрезок 
, то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяют так же, как и при вычислении значений функций.
Пример №65.3.
Вычислить интеграл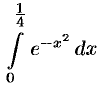 
с точностью до 
.
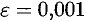Решение:
Разложим подынтегральную функцию в ряд Маклорена, заменяя на (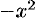
) в формуле (64.4):
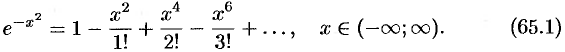
Интегрируя обе части равенства (65.1) на отрезке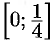 
, лежащем внутри интервала сходимости 
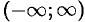, получим:
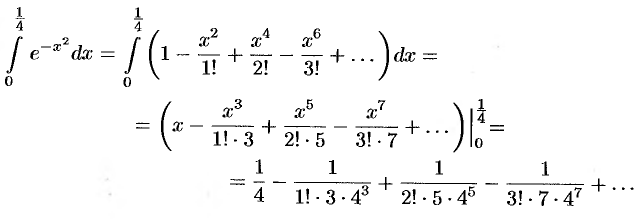
Получили ряд лейбницевского типа. Так как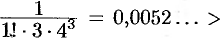 
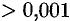, а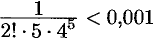 
, то с точностью до 0,001 имеем:
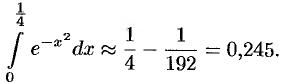
Замечание. Первообразную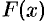 
для функции 
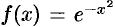легко найти в виде степенного ряда, проинтегрировав равенство (65.1) в пределах от 0 до :
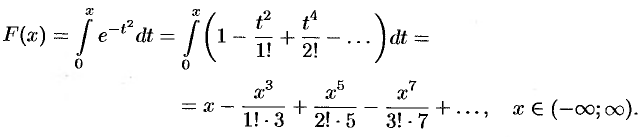
Функци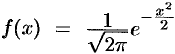и 
и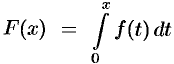 
играют очень важную роль в теории вероятностей. Первая — плотность стандартного распределения вероятностей, вторая — функция Лапласа 
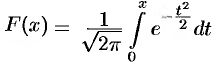(или интеграл вероятностей). Мы получили, что функция Лапласа представляется рядом
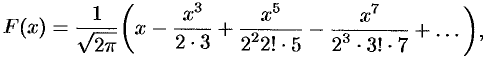
который сходится на всей числовой оси.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Разложение некоторых элементарных функций в ряд Тейлора (Маклорена) |
| Некоторые приложения степенных рядов |
| Приближенное решение дифференциальных уравнений |
| Способ последовательного дифференцирования |
