Оглавление:
Вычисление поверхностного интеграла II рода
Вычисление поверхностного интеграла II рода сводится к вычислению двойного интеграла.
Пусть функция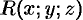 
непрерывна во всех точках поверхности 
, заданной уравнением 
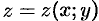, где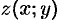 
— непрерывная функция в замкнутой области 
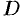(или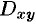 
) — проекции поверхности на плоскость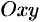 
.
Выберем ту сторону поверхности , где нормаль к ней образует с осью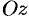 
острый угол. Тогда 
.
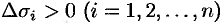Так как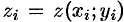 
, то интегральная сумма (58.1) может быть записана в виде
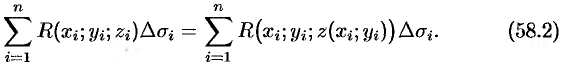
Правая часть этого равенства есть интегральная сумма для функции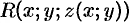 
, непрерывной в области . Переходя к пределу в равенстве (58.2) при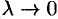 
, получаем формулу
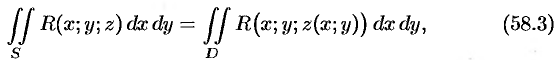
выражающую поверхностный интеграл II рода по переменным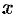 
и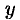 
через двойной интеграл. Если выбрать вторую сторону, т. е. нижнюю, поверхности , то полученный двойной интеграл берут со знаком «минус». Поэтому
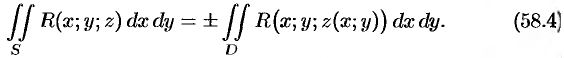
Аналогично
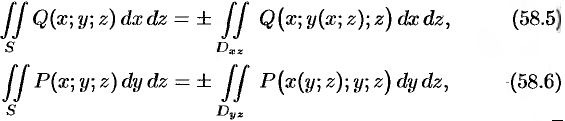
где 
и 
— проекции поверхности на плоскости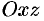 
и 
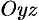соответственно (замкнутые области).
В формуле (58.5) поверхность задана уравнением 
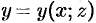, в формуле (58.6) — уравнением 
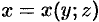. Знаки, перед интегралами выбираются в зависимости от ориентации поверхности (так, в формуле (58.5) берем знак «плюс», если нормаль к поверхности образует с осью 
острый угол, а знак «минус» — если тупой угол).
Для вычисления общего поверхностного интеграла II рода используют формулы (58.4) — (58.6), проектируя поверхность на все три координатные плоскости:
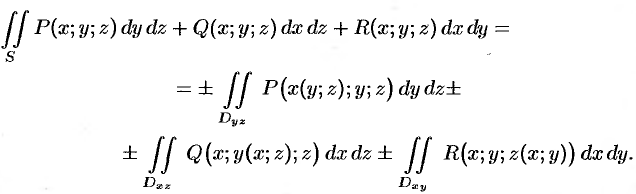
Замечание. Можно показать справедливость равенств
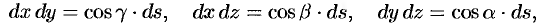
где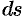 
— элемент площади поверхности ; 
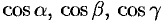— направляющие косинусы нормали 
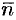к выбранной стороне поверхности .
Поверхностные интегралы I и II рода связаны соотношением
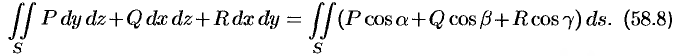
Пример №58.1.
Вычислить
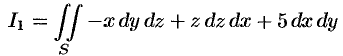
по верхней стороне части плоскости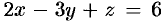 
, лежащей в IV октанте.
Решение:
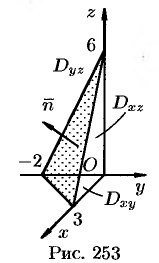
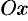На рисунке 253 изображена заданная часть плоскости. Нормаль , соответствующая указанной стороне поверхности, образует с осью тупой угол, а с осями 
и 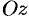— острые. В этом можно убедиться, найдя направляющие косинусы нормального вектора 
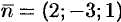плоскости:
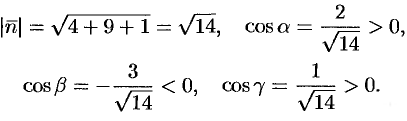
Поэтому перед двойными интегралами в формулах (58.4) и (58.6) следует брать знак «плюс», а в формуле (58.5) — знак «минус». Следовательно,
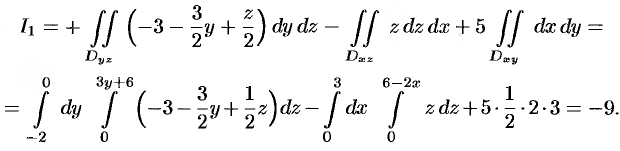
Формула Остроградского-Гаусса
Связь между поверхностным интегралом II рода по замкнутой поверхности и тройным интегралом по объему, ограниченному этой поверхностью устанавливает следующая теорема.
Теорема 58.1. Если функции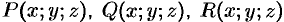 
непрерывны вместе со своими частными производными первого порядка в пространственной области 
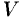, то имеет место формула
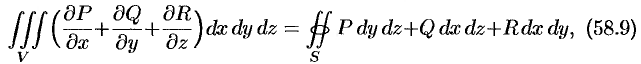
где — граница области 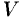и интегрирование по производится по ее внешней стороне.
Формула (58.9) называется формулой Остроградского-Гаусса (является аналогом формулы Остроградского-Грина (см. п. 56.3).
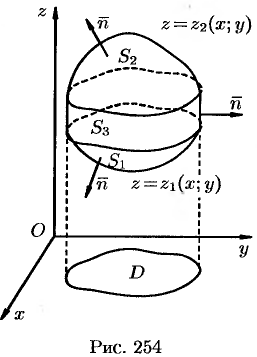
Пусть область 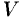ограничена снизу поверхностью 
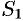, уравнение которой 
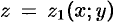; сверху — поверхностью 
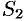, уравнение которой 
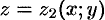(функци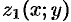и 
и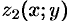 
непрерывны в замкнутой области 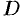— проекции 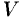на плоскость , 
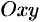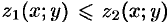); сбоку — цилиндрической поверхностью 
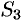, образующие которой параллельны оси (см. рис. 254).
Рассмотрим тройной интеграл
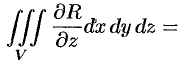
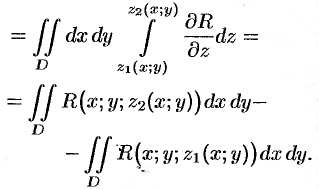
Двойные интегралы в правой части равенства заменим поверхностными интегралами II рода по внешней стороне поверхностей и соответственно (см. (58.3)). Получаем:
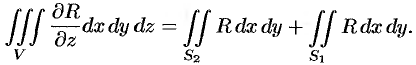
Добавляя равный нулю интеграл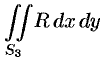 
по внешней стороне 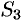(см. свойство 5 п. 58.1), получим:
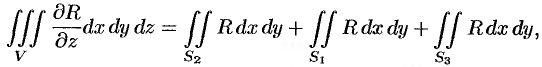
или
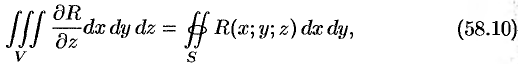
где — поверхность, ограничивающая область .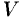
Аналогично доказываются формулы
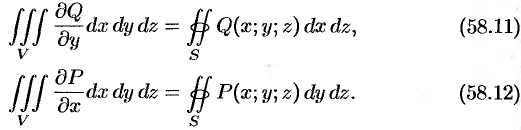
Складывая почленно равенства (58.10), (58.11) и (58.12), получаем формулу (58.9) Остроградского- Гаусса.
Замечания.
- Формула (58.9) остается справедливой для любой области , которую можно разбить на конечное число областей рассмотренного вида.
- Формулу Остроградского-Гаусса можно использовать для вычисления поверхностных интегралов II рода по замкнутым поверхностям.
Пример №58.2.
Вычислить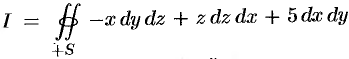 
, где — внешняя сторона пирамиды, ограниченной плоскостями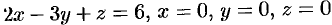 
.
Решение:
Но формуле (58.9) находим:
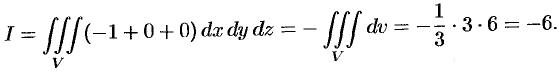
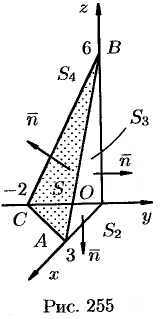
Заметим, что интеграл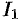 
(см. пример 58.1) можно вычислить иначе:
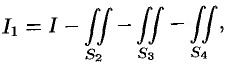
где поверхности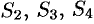 
есть соответственно треугольники 
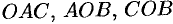(см. рис. 255).
Имеем:
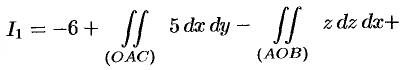
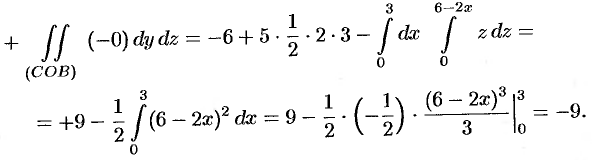
Формула Стокса
Связь между поверхностными и криволинейными интегралами II рода устанавливает следующая теорема.
Теорема 58.2. Если функци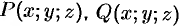и 
и 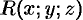непрерывны вместе со своими частными производными первого порядка в точках ориентированной поверхности , то имеет место формула
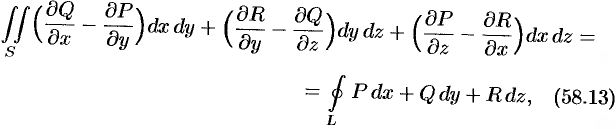
где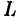 
— граница поверхности и интегрирование вдоль кривой 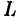производится в положительном направлении (т. е. при обходе границы 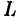поверхность должна оставаться все время слева).
Формула (58.13) называется формулой Стокса (Д. Г. Стокс — английский математик, физик).
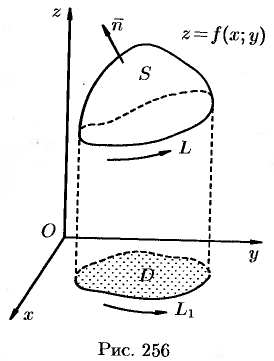
Пусть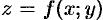 
— уравнение поверхности , функции 
, 
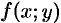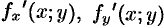непрерывны в замкнутой области 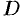(проекции поверхности на плоскость ),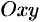 
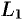— граница области 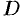(см. рис. 256). Будем считать, что поверхность пересекается с любой прямой, параллельной оси 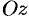, не более чем в одной точке. Выберем верхнюю сторону поверхности . Рассмотрим сначала интеграл вида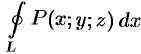 
.
Значения функции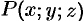 
на 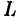равны значениям функции 
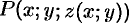на 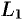. Интегральные суммы для криволинейных интегралов II рода по контурам 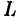и 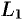совпадают. Поэтому
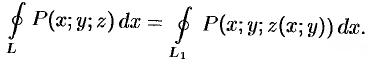
Применим к этому интегралу формулу Остроградского-Грина (см. п. 56.3). Тогда получим:
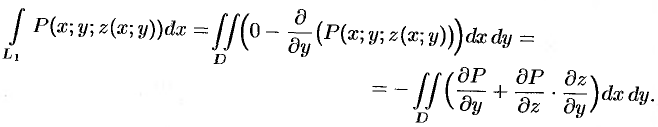
Преобразуем полученный двойной интеграл в равный ему поверхностный интеграл II рода (см. и. 58.2). Для этого последнее равенство перепишем в виде
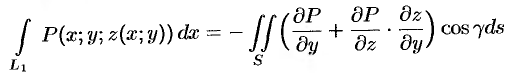
(см. 58.7) и используем уравнение нормали к поверхности (см. (45.3)). Так как выбрана верхняя сторона поверхности , т. е.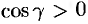 
(
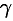— острый угол между нормалью 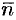к поверхности и осью 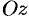), то нормаль 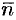и имеет проекции 
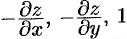. Направляющие косинусы пропорциональны соответствующим проекциям:
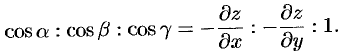
Отсюда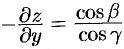 
. Тогда
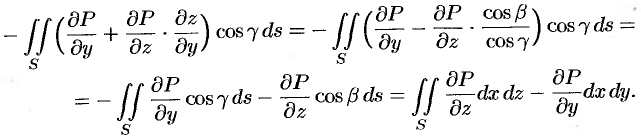
Следовательно,
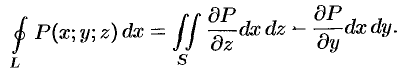
Аналогично получаются при соответствующих условиях еще два равенства:
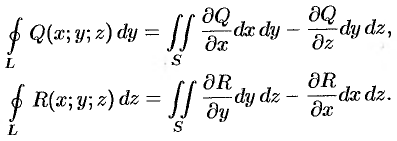
Складывая почленно три последних равенства, получаем формулу Стокса (58.13).
Отметим, что формулу Стокса (58.13) можно применить и для поверхностей более сложного вида (разбив ее на части рассмотренного выше типа).
Формулу Стокса можно применять для вычисления криволинейного интеграла по замкнутому контуру с помощью поверхностного интеграла.
Из формулы Стокса вытекает, что если выполняются условия
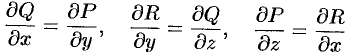
(см. п. 56.4), то криволинейный интеграл по произвольному пространственному замкнутому контуру равен нулю: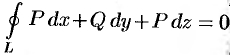 
. Следовательно, в данном случае криволинейный интеграл не зависит от вида пути интегрирования.
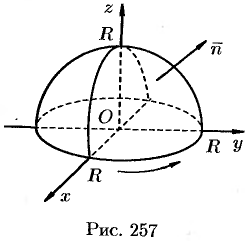
Пример №58.3.
Вычислить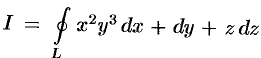 
, где контур 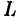— окружность 
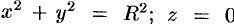: а) непосредственно, б) используя формулу Стокса, взяв в качестве поверхности полусферу 
.
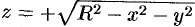Решение:
Поверхность интегрирования изображена на рисунке 257.
а) Запишем уравнение окружности в параметрической форме:
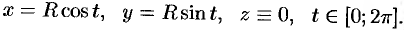
По формуле (56.7) имеем:
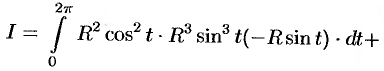
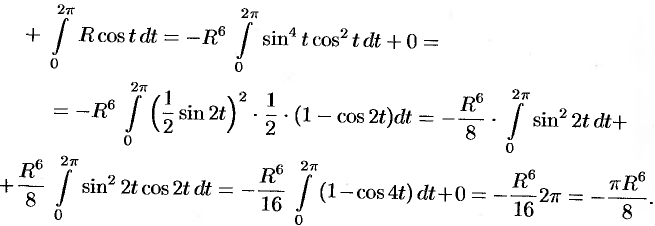
б) По формуле Стокса (58.13) находим:
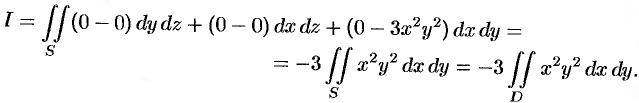
Переходя к полярным координатам, получаем:
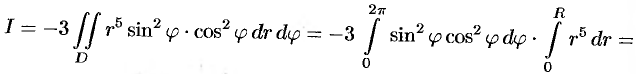
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
