Оглавление:
Некоторые приложения криволинейного интеграла II рода
Площадь плоской фигуры
Площадь  плоской фигуры, расположенной в плоскости
плоской фигуры, расположенной в плоскости 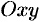 и ограниченной замкнутой линией
и ограниченной замкнутой линией  , можно найти по формуле
, можно найти по формуле
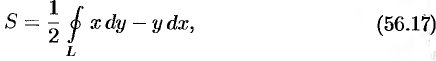
при этом кривая  обходится против часовой стрелки.
обходится против часовой стрелки.
Действительно, положив в формуле Остроградского-Грина (56.8) 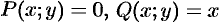 , получим:
, получим:
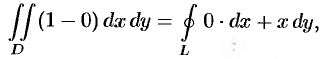
или

Аналогично, полагая 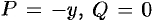 , найдем еще одну формулу для вычисления площади фигуры с помощью криволинейного интеграла:
, найдем еще одну формулу для вычисления площади фигуры с помощью криволинейного интеграла:

Сложив почленно равенства (56.18) и (56.19) и разделив на два, получим:
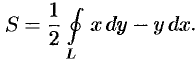
Формула (56.17) используется чаще, чем формулы (56.18) и (56.19).
Работа переменной силы
Переменная сила 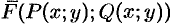 на криволинейном участке
на криволинейном участке  производит работу, которая находится по формуле
производит работу, которая находится по формуле
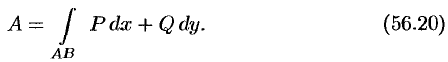
Действительно, пусть материальная точка 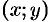 под действием поименной силы
под действием поименной силы 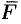 перемещается в плоскости
перемещается в плоскости 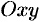 по некоторой кривой
по некоторой кривой  (от точки
(от точки  до точки
до точки 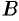 ).
).
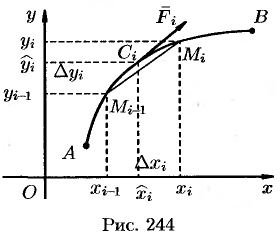
Разобьем кривую  точками
точками 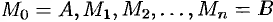 на
на  «элементарных» дуг
«элементарных» дуг 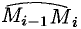 длины
длины 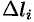 и в каждой из них возьмем произвольную точку
и в каждой из них возьмем произвольную точку 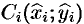 ,
,  (см.рис. 244). Заменим каждую дугу
(см.рис. 244). Заменим каждую дугу 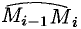 вектором
вектором 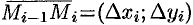 , а силу
, а силу 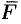 будем считать постоянной на векторе перемещения
будем считать постоянной на векторе перемещения 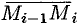 и равной заданной силе в точке
и равной заданной силе в точке 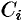 дуги
дуги 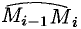 :
:
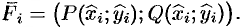
Тогда скалярное произведение 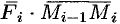 можно рассматривать как приближенное значение работы
можно рассматривать как приближенное значение работы 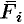 вдоль дуги
вдоль дуги 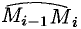 :
:
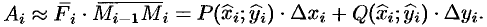
Приближенное значение работы  силы
силы 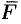 на всей кривой составит
на всей кривой составит
величину
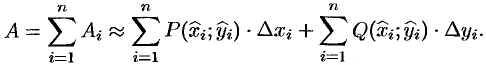
За точное значение работы  примем предел полученной суммы при
примем предел полученной суммы при 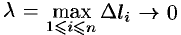 (тогда, очевидно,
(тогда, очевидно, 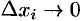 и
и 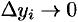 ):
):
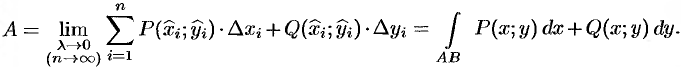
Замечание. В случае пространственной кривой  имеем:
имеем:
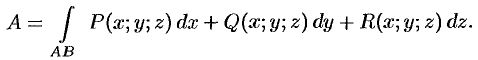
Пример №56.6.
Найти площадь фигуры, ограниченной астроидой 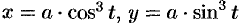 .
.
Решение:
При обхождении астроиды в положительном направлении параметр  изменяется от 0 до
изменяется от 0 до 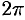 (см. рис. 245).
(см. рис. 245).
Применяя формулы (56.17) и (56.4), получим:
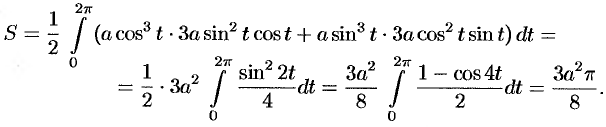
Пример №56.7.
Найти работу силы 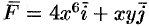 вдоль кривой
вдоль кривой 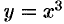 от точки
от точки 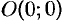 до точки
до точки 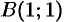 .
.
Решение:
По формуле (56.20) находим:
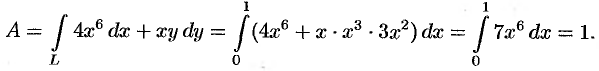
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:

