Оглавление:
Вычисление криволинейного интеграла I рода
Вычисление криволинейного интеграла I рода может быть сведено к вычислению определенного интеграла. Приведем без доказательств правила вычисления криволинейного интеграла I рода в случаях, если кривая  задана параметрическим, полярным и явным образом.
задана параметрическим, полярным и явным образом.
Параметрическое представление кривой интегрирования
Если кривая  задана параметрическими уравнениями
задана параметрическими уравнениями 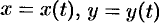 ,
, 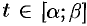 , где
, где 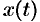 и
и 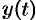 — непрерывно дифференцируемые функции параметра
— непрерывно дифференцируемые функции параметра  , причем точке
, причем точке  соответствует
соответствует 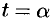 , точке
, точке 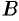 — значение
— значение 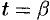 , то
, то
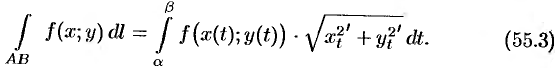
Аналогичная формула имеет место для криволинейного интеграла от функции 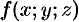 по пространственной кривой
по пространственной кривой  , задаваемой уравнениями
, задаваемой уравнениями 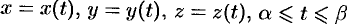 :
:
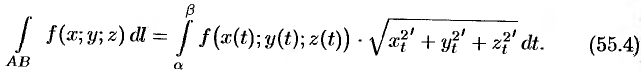
Явное представление кривой интегрирования
Если кривая  задана уравнением
задана уравнением 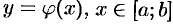 , где
, где 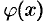 — непрерывно дифференцируемая функция, то
— непрерывно дифференцируемая функция, то
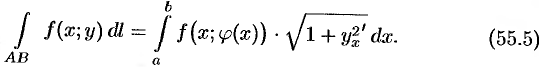
Подынтегральное выражение в правой части формулы (55.5) получается заменой в левой части 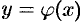 и
и 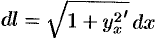 (дифференциал дуги кривой — см. п. 41.3).
(дифференциал дуги кривой — см. п. 41.3).
Пример №55.1.
Вычислить 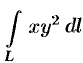 , где
, где  — отрезок прямой между точками
— отрезок прямой между точками 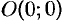 и
и 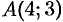 .
.
Решение:
Уравнение прямой 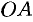 есть
есть 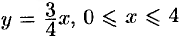 . Согласно формуле (55.5), имеем:
. Согласно формуле (55.5), имеем:
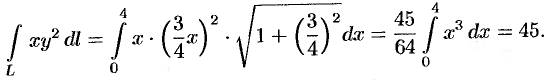
Полярное представление кривой интегрирования
Если плоская кривая  задана уравнением
задана уравнением 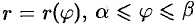 в полярных координатах, то
в полярных координатах, то 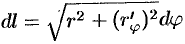 и
и
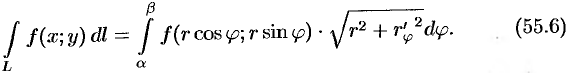
Подчеркнем, что нижний предел определенного интеграла в формулах (55.3)-(55.6) должен быть меньше верхнего.
Пример №55.2.
Вычислить 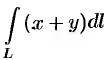 , где
, где  — лепесток лемнискаты
— лепесток лемнискаты 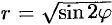 расположенной в I координатном углу.
расположенной в I координатном углу.
Решение:
Кривая интегрирования изображена на рисунке 234. Воспользуемся формулой (55.6). Так как
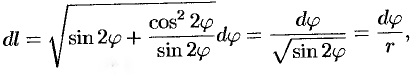
то, заметив, что 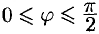 , получаем:
, получаем:
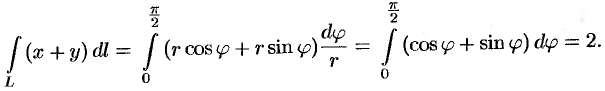
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:

