Оглавление:
Вычисление тройного интеграла в декартовых координатах
В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.
Пусть областью интегрирования  является тело, ограниченное снизу поверхностью
является тело, ограниченное снизу поверхностью 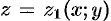 , сверху — поверхностью
, сверху — поверхностью 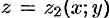 , причем
, причем 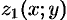 и
и 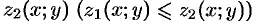 — непрерывные функции в замкнутой области
— непрерывные функции в замкнутой области  , являющейся проекцией тела на плоскость
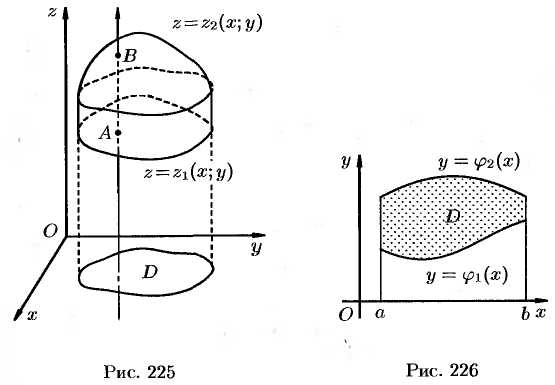
, являющейся проекцией тела на плоскость 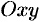 (см. рис. 225). Будем считать область
(см. рис. 225). Будем считать область  — правильней в направлении оси
— правильней в направлении оси 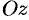 : любая прямая, параллельная оси
: любая прямая, параллельная оси 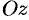 , пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области
, пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области  функции
функции 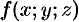 имеет место формула
имеет место формула
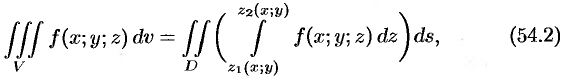
сводящая вычисление тройного интеграла к вычислению двойного интеграла от однократного (доказательство формулы (54.2) не приводим). При этом сначала вычисляется внутренний интеграл по переменной  при постоянных
при постоянных  и
и  в пределах изменения
в пределах изменения  . Нижней границей интеграла является аппликата точки
. Нижней границей интеграла является аппликата точки  — точки входа прямой, параллельной оси
— точки входа прямой, параллельной оси 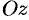 в область
в область  , т. е.
, т. е. 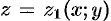 ; верхней границей — аппликата точки
; верхней границей — аппликата точки 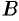 — точки выхода прямой из области
— точки выхода прямой из области  , т. е.
, т. е. 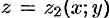 . Результат вычисления этого интеграла есть функция двух переменных:
. Результат вычисления этого интеграла есть функция двух переменных:  и
и  .
.
Если область  ограничена линиями
ограничена линиями 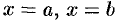 (
(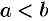 ),
), 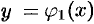 и
и 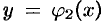 , где
, где 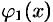 и
и 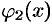 — непрерывные на отрезке
— непрерывные на отрезке  функции, причем
функции, причем 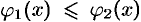 (см. рис. 226), то, переходя от двойного интеграла по области
(см. рис. 226), то, переходя от двойного интеграла по области  к повторному, получаем формулу
к повторному, получаем формулу
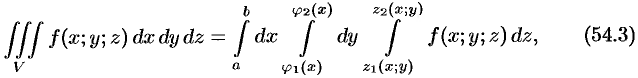
по которой вычисляется тройной интеграл в декартовых координатах.
Замечания.
- Если область
 более сложная, чем рассмотренная, то ее следует разбить на конечное число таких областей (правильных), к которым можно применить формулу (54.3).
более сложная, чем рассмотренная, то ее следует разбить на конечное число таких областей (правильных), к которым можно применить формулу (54.3). - Порядок интегрирования в формуле (54.3), при определенных условиях, может быть иным.
Пример №54.1.
Вычислить
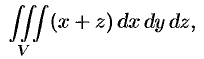
где  ограничена плоскостями
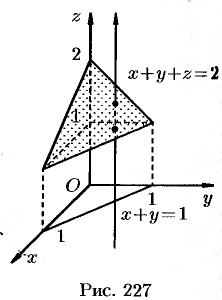
ограничена плоскостями 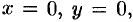
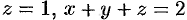 (рис. 227).
(рис. 227).
Решение:
Область  является правильной в направлении оси
является правильной в направлении оси 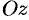 (как, заметим, и в направлении осей
(как, заметим, и в направлении осей  и
и 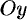 ). Ее проекция на плоскость
). Ее проекция на плоскость 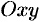 является правильной в направлении оси
является правильной в направлении оси 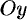 (и оси
(и оси  ). Согласно формуле (54.3), имеем:
). Согласно формуле (54.3), имеем:
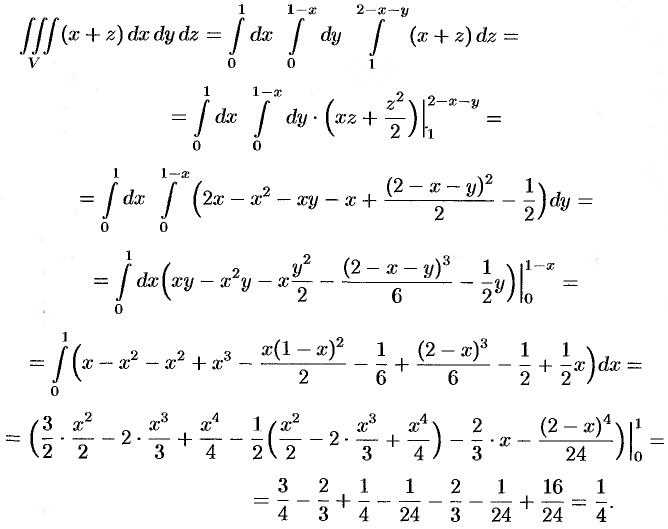
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Вычисление двойного интеграла в полярных координатах |
| Приложения двойного интеграла |
| Вычисление тройного интеграла в цилиндрических и сферических координатах |
| Некоторые приложения тройного интеграла |

