Пример №52.2.
Решить систему уравнений:
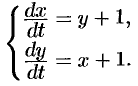
Решение:
Сложим почленно данные уравнения: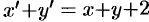 
, или 
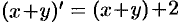. Обозначим 
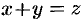. Тогда имеем 
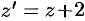. Решаем полученное уравнение: 
, 
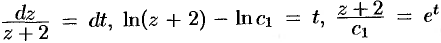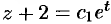или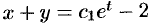 
.
Получили так называемый первый интеграл системы. Из него можно выразить одну из искомых функций через другую, тем самым уменьшить на единицу число искомых функций. Например,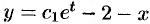 
. Тогда первое уравнение системы примет вид
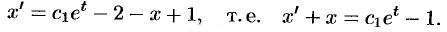
Найдя из него 
(например, с помощью подстановки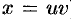 
), найдем и 
.
Замечание. Данная система «позволяет» образовать еще одну интегрируемую комбинацию: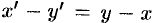 
, т. е. 
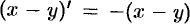. Положив 
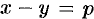, имеем: 
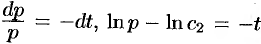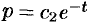, или 
, 
, или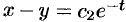 
. Имея два первых интеграла системы, т. е. 
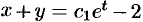и 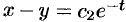, легко найти (складывая и вычитая первые интегралы), что 
.
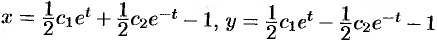Благодаря этой странице вы научитесь сами решать такие примеры, на ней содержится полный курс лекций с примерами решения:
Другие примеры с решением возможно вам они будут полезны:
