Пример №48.7.
Найти общий интеграл уравнения
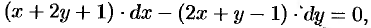
т.е. 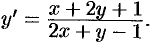
Решение:
Положив 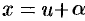 ,
, 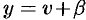 , получаем:
, получаем:
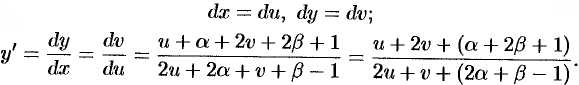
Подберем 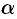 и
и 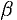 так, чтобы
так, чтобы
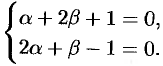
Находим, что 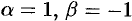 . Заданное уравнение примет вид
. Заданное уравнение примет вид
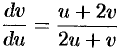
и будет являться однородным. Его решение получается, как это было показано выше, при помощи подстановки 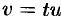 . Заметим, что, решив его, следует заменить
. Заметим, что, решив его, следует заменить 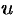 и
и 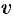 соответственно на
соответственно на  и
и 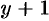 . В итоге получим
. В итоге получим 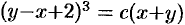 — общий интеграл данного уравнения.
— общий интеграл данного уравнения.
Благодаря этой странице вы научитесь сами решать такие примеры, на ней содержится полный курс лекций с примерами решения:
Другие примеры с решением возможно вам они будут полезны:

