Однополостный гиперболоид
Исследуем поверхность, заданную уравнением
Пересекая поверхность (12.30) плоскостью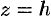 
, получим линию пересечения, уравнения которой имеют вид
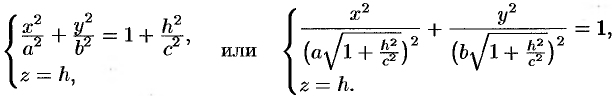
Как видно, этой линией является эллипс с полуосями
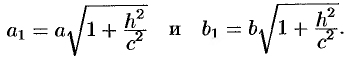
Полуоси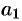 
и 
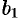достигают своего наименьшего значения при 
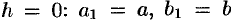. При возрастании 
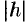полуоси эллипса будут увеличиваться.
Если пересекать поверхность (12.30) плоскостям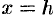и 
или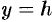 
, то в сечении получим гиперболы. Найдем, например, линию пересечения поверхности (12.30) с плоскостью 
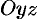, уравнение которой 
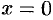. Эта линия пересечения описывается уравнениями
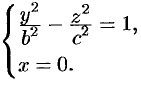
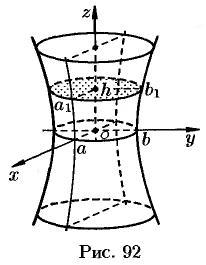
Как видно, эта линия есть гипербола (см. рис. 92).
Анализ этих сечений показывает, что поверхность, определяемая уравнением (12.30), имеет форму бесконечной расширяющейся трубки. Поверхность (12.30) называется однополостным гиперболоидом.
Замечание: можно доказать, что через любую точку гиперболоида (12.30) проходят две прямые, лежащие на нем.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Нормальное уравнение плоскости |
| Эллипсоид |
| Двухполостный гиперболоид |
| Эллиптический параболоид |
