Уравнение плоскости в отрезках
Пусть плоскость отсекает на осях  и
и 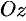 соответственно отрезки
соответственно отрезки 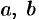 и
и 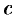 , т. е. проходит через три точки
, т. е. проходит через три точки 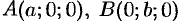 и
и 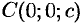 (см. рис. 70).
(см. рис. 70).
Подставляя координаты этих точек в уравнение (12.6), получаем
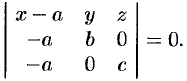
Раскрыв определитель, имеем 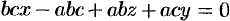 , т. е.
, т. е. 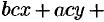
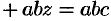 или
или

Уравнение (12.7) называется уравнением плоскости в отрезках на осях. Им удобно пользоваться при построении плоскости.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Дополнительные сведения о гиперболе |
| Уравнение плоскости, проходящей через три данные точки |
| Нормальное уравнение плоскости |
| Эллипсоид |

