Уравнение плоскости, проходящей через три данные точки
Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдем уравнение плоскости 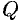 , проходящей через три данные точки
, проходящей через три данные точки 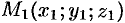 ,
, 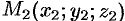 и
и 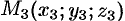 , не лежащие на одной прямой.
, не лежащие на одной прямой.
Возьмем на плоскости произвольную точку 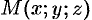 и составим векторы
и составим векторы 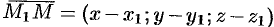 ,
, 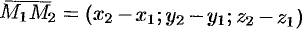 ,
, 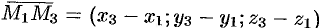 . Эти векторы лежат на плоскости
. Эти векторы лежат на плоскости 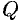 , следовательно, они компланарны. Используем условие компланарности трех векторов (их смешанное произведение равно нулю), получаем
, следовательно, они компланарны. Используем условие компланарности трех векторов (их смешанное произведение равно нулю), получаем
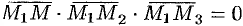 , т.е.
, т.е.
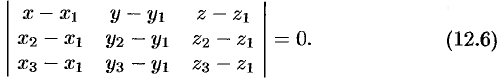
Уравнение (12.6) есть уравнение плоскости, проходящей через три данные точки.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Уравнение равносторонней гиперболы, асимптотами которой служат оси координат |
| Дополнительные сведения о гиперболе |
| Уравнение плоскости в отрезках |
| Нормальное уравнение плоскости |

