Уравнение равносторонней гиперболы, асимптотами которой служат оси координат
Гипербола (11.9) называется равносторонней, если ее полуоси равны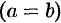 
. Ее каноническое уравнение
Асимптоты равносторонней гиперболы имеют уравнения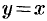 
и 
и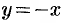, следовательно, являются биссектрисами координатных углов.
Рассмотрим уравнение этой гиперболы в новой системе координат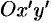 
(см. рис. 58), полученной из старой поворотом осей координат на угол 
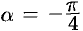. Используем формулы поворота осей координат (их вывод показан на с. 63):
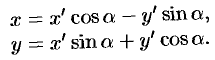
Подставляем значения 
и 
в уравнение (11.12):
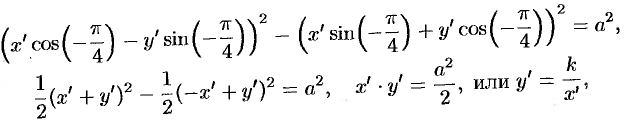
где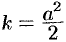 
.
Уравнение равносторонней гиперболы, для которой ос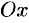и 
и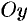 
являются асимптотами, будет иметь вид 
.
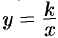На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Исследование формы эллипса по его уравнению |
| Дополнительные сведения об эллипсе |
| Дополнительные сведения о гиперболе |
| Парабола |
