Полярное уравнение прямой
Найдем уравнение прямой в полярных координатах. Ее положение можно определить, указав расстояние 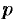 от полюса
от полюса 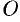 до данной прямой и угол
до данной прямой и угол 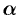 между полярной осью
между полярной осью 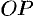 и осью
и осью 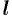 , проходящей через полюс
, проходящей через полюс 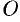 перпендикулярно данной прямой (см. рис. 44).
перпендикулярно данной прямой (см. рис. 44).
Для любой точки 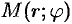 на данной прямой имеем:
на данной прямой имеем:
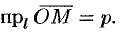
С другой стороны,
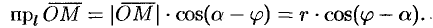
Следовательно,

Полученное уравнение (10.10) и есть уравнение прямой в полярных координатах.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Уравнение прямой в отрезках |
| Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору |
| Нормальное уравнение прямой |
| Исследование формы эллипса по его уравнению |

