Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
Найдем уравнение прямой, проходящей через заданную точку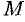 
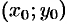перпендикулярно данному ненулевому вектору 
.
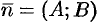Возьмем на прямой произвольную точку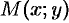 
и рассмотрим вектор 
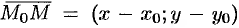(см. рис. 43). Поскольку векторы 
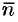и 
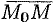перпендикулярны, то их скалярное произведение равно нулю: 
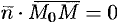, то есть
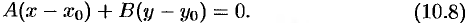
Уравнение (10.8) называется уравнением, прямой, проходящей через заданную точку перпендикулярно заданному вектору.
Вектор 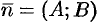, перпендикулярный прямой, называется нормальным вектором этой прямой.
Уравнение (10.8) можно переписать в виде
где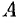 
и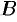 
— координаты нормального вектора, 
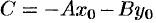— свободный член. Уравнение (10.9) есть общее уравнение прямой
(см. (10.4)).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Уравнение прямой, проходящей через две точки |
| Уравнение прямой в отрезках |
| Полярное уравнение прямой |
| Нормальное уравнение прямой |
