Оглавление:
Рассмотрим функцию, заданную равенством 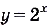 . Составим таблицу её значений для нескольких значений аргумента:
. Составим таблицу её значений для нескольких значений аргумента:
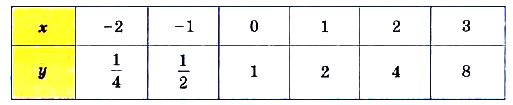
На рисунке 19, а обозначены точки, координаты которых соответствуют этой таблице. Когда на этой же координатной плоскости обозначить больше точек с координатами х, у, удовлетворяющих равенству 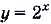 , они разместятся, как показано на (рис 19, б). А если для каждого действительного значения х вычислить соответствующее значение у и обозначить на координатной плоскости точки с координатами х и у, они разместятся на одной бесконечной кривой (рис. 19 в). Эта кривая — график функции
, они разместятся, как показано на (рис 19, б). А если для каждого действительного значения х вычислить соответствующее значение у и обозначить на координатной плоскости точки с координатами х и у, они разместятся на одной бесконечной кривой (рис. 19 в). Эта кривая — график функции 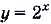
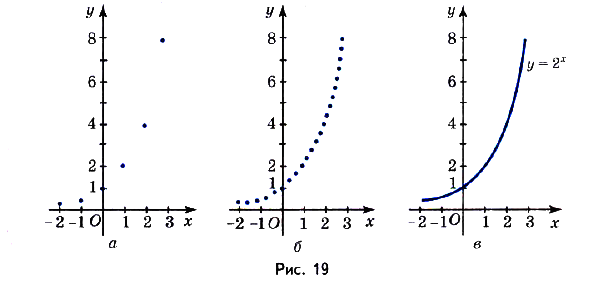
График функции 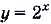 размещён в I и II координатных четвертях. Когда
размещён в I и II координатных четвертях. Когда 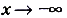 , он как угодно близко подходит к оси Ох, но общих точек с ней не имеет. Говорят, что график функции
, он как угодно близко подходит к оси Ох, но общих точек с ней не имеет. Говорят, что график функции  асимптотически приближается к оси Ох, что ось Ох — асимптота этого графика. Когда х неограниченно увеличивается, график функции
асимптотически приближается к оси Ох, что ось Ох — асимптота этого графика. Когда х неограниченно увеличивается, график функции 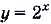 всё дальше отходит от оси Ох. Как видим, функция
всё дальше отходит от оси Ох. Как видим, функция 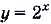 определена для всех действительных чисел, её область значений — промежуток
определена для всех действительных чисел, её область значений — промежуток 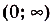 На всей области определения функция возрастает, она ни чётная, ни нечётная, ни периодическая.
На всей области определения функция возрастает, она ни чётная, ни нечётная, ни периодическая.
Рассматриваемая функция 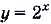 — пример показательной функции, а именно — показательная функция с основанием 2.
— пример показательной функции, а именно — показательная функция с основанием 2.
Показательной функцией называется функция, заданная формулой 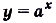 , где
, где 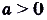 и
и 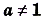 .
.
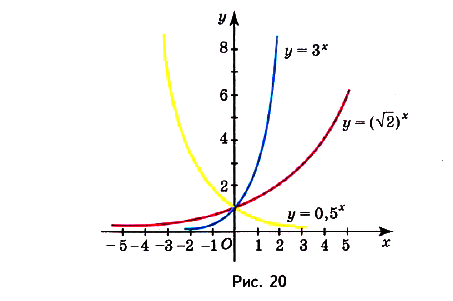
Примеры других показательных функций: 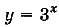 ,
, 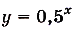 ,
, 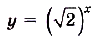 . Их графики изображены на (рис20). Согласно определению функция
. Их графики изображены на (рис20). Согласно определению функция 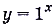 не является показательной.
не является показательной.
Свойства показательной функции
1) Область определения функции 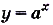 — множество R, ибо при каждом положительном а и действительном х выражение
— множество R, ибо при каждом положительном а и действительном х выражение 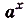 определено.
определено.
2) Область значений функции 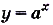 — множество
— множество 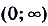 поскольку, если основание а степени положительное, то положительная и степень ах. Следовательно, функция
поскольку, если основание а степени положительное, то положительная и степень ах. Следовательно, функция 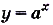 принимает только положительные значения.
принимает только положительные значения.
3) Если 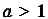 , функция
, функция 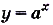 возрастает, а если
возрастает, а если 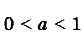 — убывает. Это свойство хорошо видно на графиках функций (рис. 20).
— убывает. Это свойство хорошо видно на графиках функций (рис. 20).
4) Функция 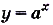 каждое своё значение принимает только один раз, т. е. прямую, параллельную оси Ох, график показательной функции может пересечь только в одной точке. Это следует из свойства 3.
каждое своё значение принимает только один раз, т. е. прямую, параллельную оси Ох, график показательной функции может пересечь только в одной точке. Это следует из свойства 3.
5)Функция 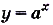 ни чётная, ни нечётная, ни периодическая. Поскольку каждое своё значение она принимает только один раз, то не может быть чётной или периодической. Не может она быть и нечётной, так как не имеет ни отрицательных, ни нулевых значений.
ни чётная, ни нечётная, ни периодическая. Поскольку каждое своё значение она принимает только один раз, то не может быть чётной или периодической. Не может она быть и нечётной, так как не имеет ни отрицательных, ни нулевых значений.
6) График каждой показательной функции проходит через точку А (0, 1), поскольку если 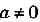 то
то 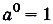 .
.
При решении задач и упражнений, связанных с показательной функцией, особенно часто используется третье свойство, в котором указывается на монотонность показательной функции, то есть её возрастание или убывание. В частности из него вытекают следующие утверждения.
- Если
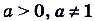 и
и 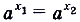 , то
, то 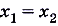 .
. - Если
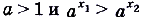 , то
, то 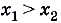 .
. - Если
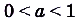 и
и 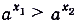 , то
, то 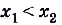
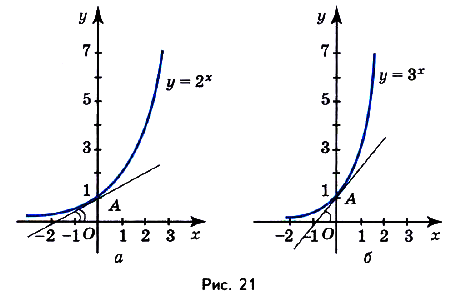
Присмотритесь к графикам показательных функций 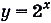 и
и 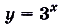 (рис. 21). Угловой коэффициент касательной, проведённой в точке А (0; 1) к графику функции
(рис. 21). Угловой коэффициент касательной, проведённой в точке А (0; 1) к графику функции 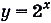 меньше 1, а к графику функции
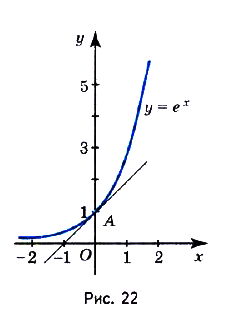
меньше 1, а к графику функции 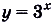 — больше 1. Существует ли такая показательная функция, у которой угловой коэффициент касательной к её графику в точке А (0,1) равен 1? Существует (рис. 22).Основание этой показательной функции — иррациональное число 2,71828…, которое принято обозначать буквой е. Показательная функция
— больше 1. Существует ли такая показательная функция, у которой угловой коэффициент касательной к её графику в точке А (0,1) равен 1? Существует (рис. 22).Основание этой показательной функции — иррациональное число 2,71828…, которое принято обозначать буквой е. Показательная функция 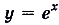 в математике и многих прикладных науках
в математике и многих прикладных науках
встречается довольно часто, её называют экспонентои. (лат. exponens — выставлять напоказ).
^ К показательной функции иногда относят также функции вида 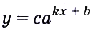 . При помощи таких функций описывают много разных процессов, связанных с физикой, химией, биологией, экономикой, социологией и т. д. Например, процессы новообразования и распада вещества можно описать с помощью формулы
. При помощи таких функций описывают много разных процессов, связанных с физикой, химией, биологией, экономикой, социологией и т. д. Например, процессы новообразования и распада вещества можно описать с помощью формулы 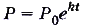 Здесь Р —количество вновь образованного (или распавшегося) вещества в момент времени
Здесь Р —количество вновь образованного (или распавшегося) вещества в момент времени 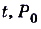 — начальное количество вещества, k — постоянная, значение которой определяется для конкретной ситуации. Подберите самостоятельно соответствующие примеры.
— начальное количество вещества, k — постоянная, значение которой определяется для конкретной ситуации. Подберите самостоятельно соответствующие примеры.
Примеры с решением
Пример №1
Сравните с единицей число: а) 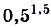 ; б)
; б) 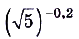 .
.
Решение:
а) Представим число 1 в виде степени с основанием 0,5. Имеем: 1 = 0,5°. Поскольку функция 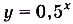 — убывающая и 1,5 > 0, то
— убывающая и 1,5 > 0, то 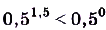 , отсюда
, отсюда 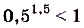 ;
;
б)  ;
;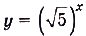 — функция возрастающая и —0,2 < О, поэтому
— функция возрастающая и —0,2 < О, поэтому 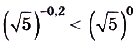 , отсюда
, отсюда 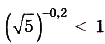 .
.
Пример №2
Функция 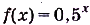 задана на промежутке [-2; 3]. Найдите её наименьшее и наибольшее значения.
задана на промежутке [-2; 3]. Найдите её наименьшее и наибольшее значения.
Решение:
Поскольку 0,5 < 1, то данная функция убывающая. Поэтому её наименьшее и наибольшее значения:
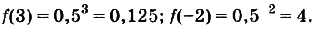
Пример №3
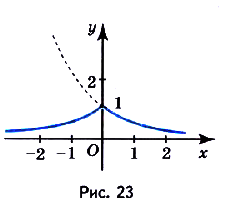
Постройте график функции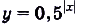
Решение:
Функция 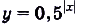 —
—
чётная (проверьте). График чётной
функции симметричен относительно оси Оу, поэтому достаточно построить график заданной функции для 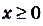 и отобразить его симметрично относительно оси Оу. Если
и отобразить его симметрично относительно оси Оу. Если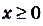 , то
, то 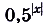
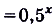 . Построим график функции
. Построим график функции 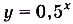 для х > 0 и отобразим его симметрично относительно оси Оу (рис. 23).
для х > 0 и отобразим его симметрично относительно оси Оу (рис. 23).
Пример №4
Найти асимптоты графика функции:
а) 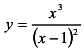 ; б)
; б) 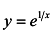 ; в)
; в) 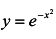 ; г)
; г) 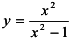 .
.
Решение:
Нахождение асимптот кривой (если они имеются) является одним из шагов схемы полного исследования функции.
Если функция имеет точки бесконечного разрыва, то график функции имеет вертикальные асимптоты. Наклонные асимптоты (невертикальные) имеют вид: 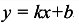 где
где 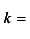
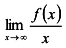
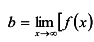
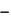
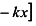 , если последние пределы существуют.
, если последние пределы существуют.
Пределы надо вычислить отдельно при ;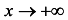 и при
и при 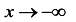 . Наклонных асимптот может быть не более двух (правая, левая), а) Вычислим пределы данной функции при х —> 1:
. Наклонных асимптот может быть не более двух (правая, левая), а) Вычислим пределы данной функции при х —> 1:
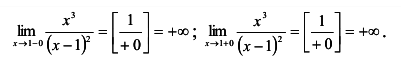
Так как односторонние пределы при х —>1 бесконечны, то х = 1 — точка бесконечного разрыва; х = 1 — вертикальная асимптота кривой 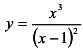 Вычислим пределы:
Вычислим пределы:
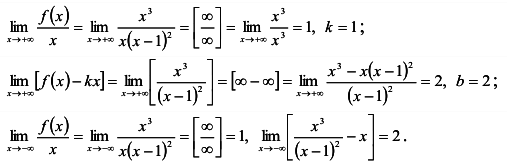
У кривой 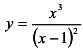 правая и левая асимптоты совпадают;
правая и левая асимптоты совпадают;
наклонная асимптота задается уравнением у = х + 2. б) Вертикальная асимптота кривой 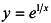 может быть только в точке х= 0.
может быть только в точке х= 0.
Вычислим пределы: 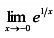
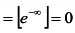 ,
, 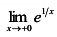
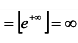 .
.
В точке x = 0 функция 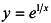 имеет бесконечный разрыв. Поэтому х = = 0 -уравнение вертикальной асимптоты графика данной функции. Вычислим пределы:
имеет бесконечный разрыв. Поэтому х = = 0 -уравнение вертикальной асимптоты графика данной функции. Вычислим пределы:
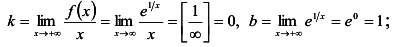
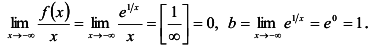
Следовательно, данная кривая имеет одну асимптоту у = 1. Эту асимптоту называют горизонтальной.
в) Данная функция определена и непрерывна на всей числовой оси, вертикальных асимптот график функции не имеет.
Найдем предел 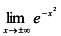
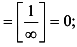
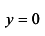 горизонтальная асимптота.
горизонтальная асимптота.
г) Данную функцию можно записать в виде 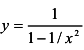 откуда видно, что
откуда видно, что 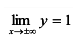 , то есть
, то есть 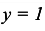 горизонтальная асимптота графика функции.
горизонтальная асимптота графика функции.
Так как 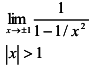
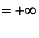 ,
, 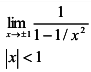
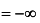 то график данной функции имеет две вертикальные асимптоты (см. рис. 2)
то график данной функции имеет две вертикальные асимптоты (см. рис. 2)
Пример №5
Исследовать функцию и построить ее график:
а) 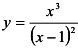 ; б)
; б) 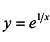 .
.
Решение:
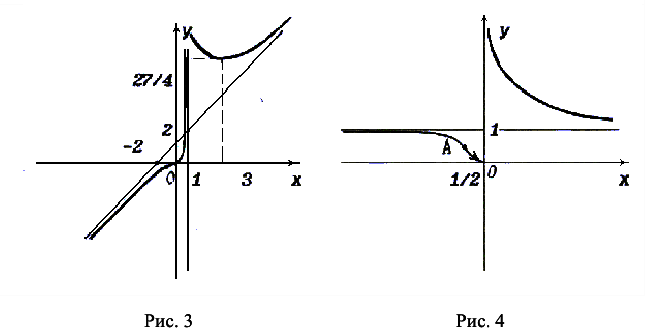
Выполним исследование функций по схеме исследования, а) Данная функция не определена при х = 1. В предыдущей задаче для этой функции установлено, что х = 1 — вертикальная асимптота, а у= х + 2 -наклонная асимптота графика функции.
Очевидно, что данная функция не является ни четной, ни нечетной , ни периодической.
Найдем точки пересечения графика функции с осями координат: если х = 0, то у = 0 -> 0(0, 0) лежит на графике; если у = 0, то х = 0, то есть 0(0,0) единственная точка пересечения графика функции с осями координат.
Найдем промежутки монотонности функции:
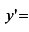
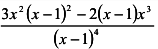
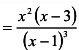 ; критические точки первого рода
; критические точки первого рода 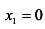 ;
;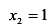 ;
;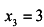 .
.

Найдем промежутки выпуклости (вогнутости), точки перегиба:
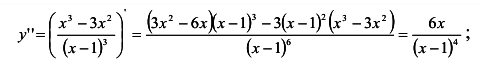
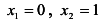 — критические точки второго рода .
— критические точки второго рода .

Из таблиц видно, что функция имеет минимум при х = 0 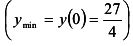 , график функции имеет одну точку перегиба 0(0; 0).
, график функции имеет одну точку перегиба 0(0; 0).
В задаче 1 а) были найдены асимптоты кривой 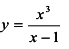 (х = 1 и у =х + 2).
(х = 1 и у =х + 2).
Выявленные свойства функции позволяют построить ее график (рис). 3
б) Данная функция определена при 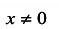 .
.
Вычислим пределы функции при стремлении х к границам области определения:
 ;
;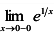
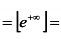
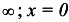 — вертикальная асимптота;
— вертикальная асимптота;
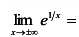
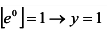 — горизонтальная асимптота графика функции.
— горизонтальная асимптота графика функции.
Исследуем функцию на возрастание (убывание), экстремум: 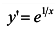
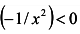 функция убывает во всей области определения.
функция убывает во всей области определения.
Так как 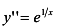
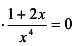 х = -1/2, и у» меняет знак с минуса на плюс в окрестности точки х = -1/2, то точка
х = -1/2, и у» меняет знак с минуса на плюс в окрестности точки х = -1/2, то точка 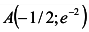 является точкой перегиба графика функции. При х > 0у» > 0, поэтому на промежутке
является точкой перегиба графика функции. При х > 0у» > 0, поэтому на промежутке 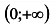 график функции имеет вогнутость. Примерный график функции приведен на рис.4.
график функции имеет вогнутость. Примерный график функции приведен на рис.4.
Пример №6
Исследовать функцию методами дифференциального исчисления и построить ее график. Исследование функции и построение графика рекомендуется провести по следующей схеме:
1) найти область определения функции D(y);
2) найти точки пересечения графика функции с осями координат.
3) исследовать функцию на непрерывность; найти точки разрыва функции и её односторонние пределы в точках разрыва;
4) найти асимптоты графика функции;
5) найти точки экстремума функции и определить интервалы её монотонности;
6) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика;
7) построить график, используя результаты предыдущих исследований;
8) найти наибольшее и наименьшее значения на отрезке 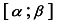
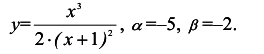
Решение:
1.Область определения: 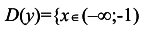
 .
.
2.Точки пересечения графика функции с осями координат.
Для нахождения точек пресечения с осью Оx возьмем у=0 и решим уравнение 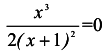 . Получим
. Получим 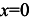 , то есть точкой пересечения графика функции с осью Ох является точка 0(0;0). Эта же точка является точкой пересечения с осью 0у, так как у(0)=0.
, то есть точкой пересечения графика функции с осью Ох является точка 0(0;0). Эта же точка является точкой пересечения с осью 0у, так как у(0)=0.
3. Исследование на непрерывность и классификация точек разрыва. Заданная функция непрерывна всюду, кроме точки х=-1. Вычислим её односторонние пределы в этой точке:
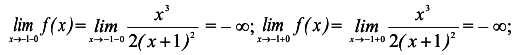
Таким образом, точка x=-1 является для заданной функции точкой разрыва второго рода, а прямая х=-1— вертикальной асимптотой графика.
4.Исследование графика на наличие наклонных асимптот:
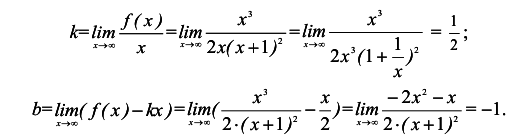
Таким образом, прямая 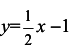 — наклонная асимптота графика.
— наклонная асимптота графика.
5. Исследование на экстремум и промежутки монотонности.
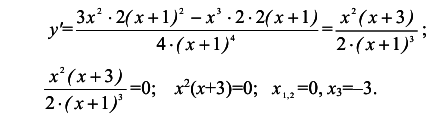
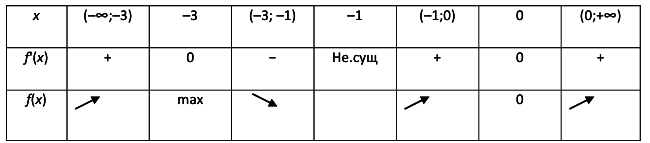
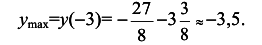
6. Исследование графика на выпуклость, вогнутость, точки перегиба.
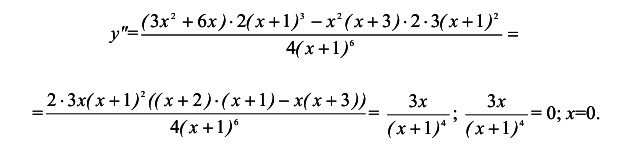
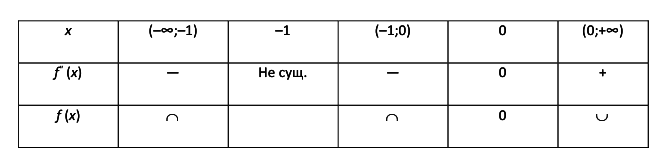
0(0;0) — точка перегиба графика функции.
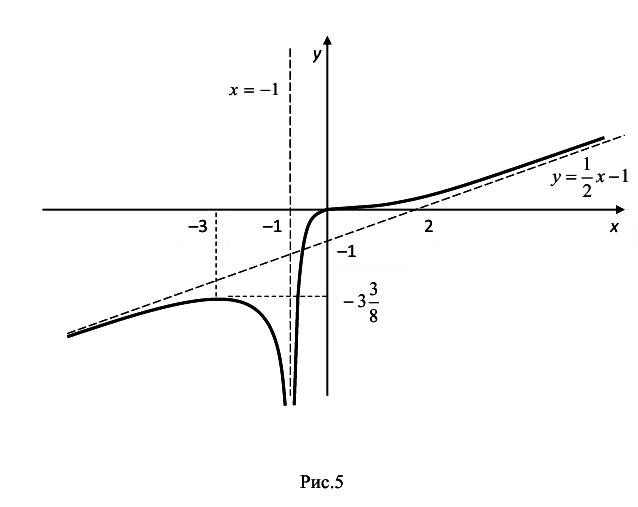
7. Построение графика.
График имеет вид, представленный на рис 5.
8. Найдем наибольшее и наименьшее значения заданной функции на отрезке [-5; -2]. Для этого подсчитаем значения функции на концах этого отрезка, в стационарных точках, попавших на отрезок, и сравним результаты:
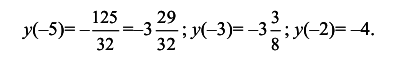
Итак, 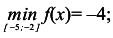
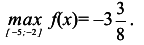
Пример №7
Вычислить приращение и дифференциал функции 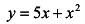 при
при 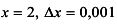 . Найти абсолютную и относительную погрешности при замене приращения функции дифференциалом.
. Найти абсолютную и относительную погрешности при замене приращения функции дифференциалом.
Решение:
Вычислим приращение функции:
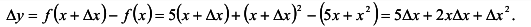
Вычислим дифференциал функции: 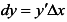
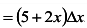 . При х = 2,
. При х = 2, 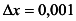 получаем:
получаем:
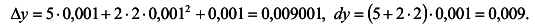
Подсчитаем погрешности приближенной формулы 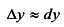 : абсолютная погрешность
: абсолютная погрешность 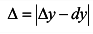
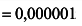 ; относительная погрешность
; относительная погрешность 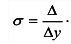
Пример №8
Вычислить дифференциалы функций:
а) 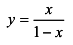 б)
б) 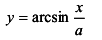 ; в)
; в) 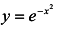 ; г)
; г) 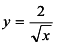 .
.
Решение:
Воспользуемся инвариантной формой дифференциала 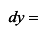
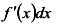
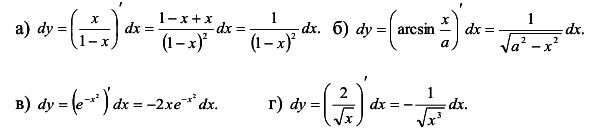
Замечание. Если x — независимая переменная величина, то 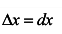
Пример №9
Вычислить приближенно:
а) 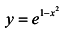 при х = 1, 05; б)
при х = 1, 05; б) 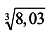 ; в)
; в) 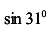 .
.
Решение:
Воспользуемся формулой:
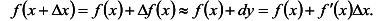
а) Имеем 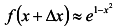
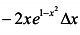 откуда при
откуда при 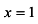 ,
,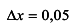 получаем
получаем 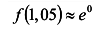
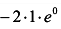
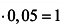
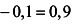 .
.
б) 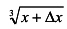
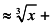
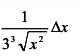 , откуда при
, откуда при 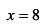 ,
, 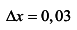 , получаем
, получаем 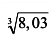
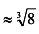
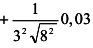
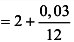
в) 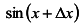
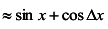 , откуда при х = 30°
, откуда при х = 30° 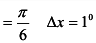
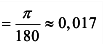 получаем
получаем 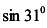
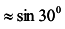
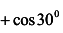
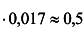
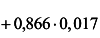
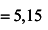 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Первообразная и интеграл |
| Функции и их основные свойства |
| Предел последовательности |
| Степени с действительными показателями |

