Оглавление:






Энтропия.
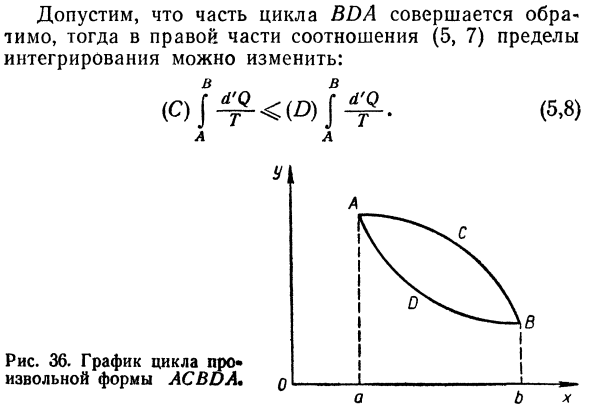
- Энтропия Понятие энтропии Самое сложное понятие физики. Энтропия в переводе с греческого Греческое слово (ettpco) означает изменение в одном направлении. Во-первых, энтропия была официально введена в науку. Затем, основываясь на ряде исследований Физическое содержание делало задачу ясной. Примените второй закон термодинамики к циклу Любая форма ADBCA (рисунок 36).
В этом цикле интегралы являются D’Q I-Y * — преобразуется в 2 члена, соответствующие Часть цикла: DIA и BDA. Е, 6) © и (D) относятся к интеграционному пути. Соотношение* Решение Е, 6) может быть представлено по-разному следующим образом: Форма: Е, 7) Предположим, что часть цикла BDA завершена Правая сторона отношения Е, то обратимая, 7) предел Интеграция может быть изменена: В Рисунок 36.Расписание цикла о Любая форма Асвии. Икс Сто семнадцать Это становится выражением второго закона термодинамики. Термодинамика цикла в наиболее распространенных случаях.
Интеграл не зависит от пути Потому что пометка, и DIA и BDA path были нами После того, как был выбран совершенно произвольно. Людмила Фирмаль
Здесь мы рассматриваем только обратимые процессы. Полученное уравнение имеет вид、 d’Q В процессе, — j? 、 В E, 9) для J-jr-обратимый процесс Один Только от начального и конечного состояния системы. Таким образом, подынтегральное выражение — ^явно Вся производная зависимой функции. Только от состояния системы. Это очевидная особенность Состояние указывалось в S и называлось энтропией. * Сосед Что ж… 、 В © ДЖ *? e (D)J ^ H = SB-SA. Е, 90 А. А. Возвращение к рассмотрению общего дела( Формула 5, 8).
Потому что правый интеграл от E записывается как 8) В случае обратимого процесса его можно заменить другим Разница SB-SA: В (Д) Я. В. СБ-Са, Е, 10) Один Или, если дается любой выбор цикла: В — СА. Электронная, 11) Формула Е, 11), Тер- Термодинамика в наиболее распространенных случаях, которые не связаны Не только для циклов, но и для открытых процессов. 118.
- Формула E, 5) легко получается из Формулы E, I Особый случай. Например, для закрытого процесса Так… Oo Ji z==: U и 2-й закон термодинамики в виде е 11) утверждается Разница между энтропией 2 состояний системы d’Q Равен Интегралу-jr-между этими состояниями、 Если последнее принимается обратимым образом d’Q l Интеграл от Y по необратимому пути.
Однако это не означает разницы между энтропией Оно имеет различное значение в зависимости от Рассматриваемые процессы (обратимые или необратимые Необратимый.)Знак Неравенство Формулы E\) имеет вид、 В случае необратимого процесса Интеграл слева Мы больше не представляем разницу в энтропии、 Ее.
Энтропия-это отдельная функция Разница между состоянием и, следовательно, энтропией постоянна Постоянное значение независимо от характера процесса. Людмила Фирмаль
Второй закон термодинамики дифференцирования Форма есть форма: ^ — <ДС Е, 12) Использование первого количественного выражения Начало термодинамики B, 8), получаем основное уравнение Следующие формы термодинамики: (^^Е, 13)
Смотрите также:
Решение задач по термодинамике

