Оглавление:













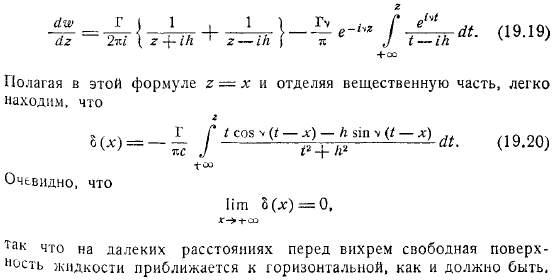



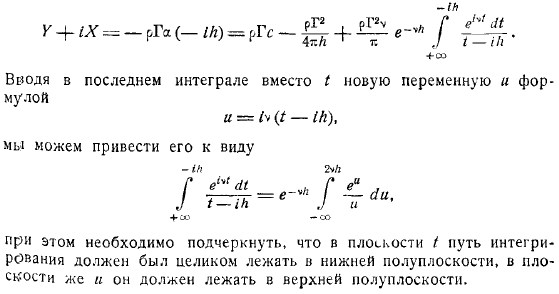



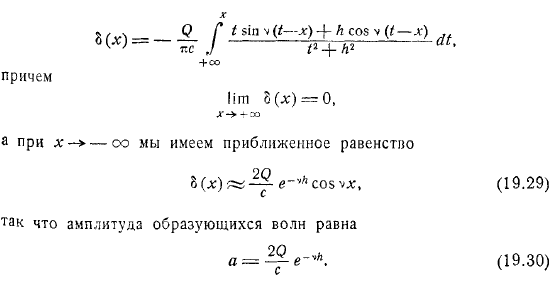









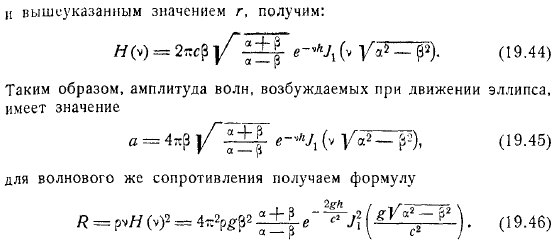

Волновое сопротивление. Движение тела под свободной поверхностью
Проблема волнового сопротивления в гидромеханике тесно связана с проблемой передачи энергии волнами. Например, предположим, что за кораблем, движущимся с определенной скоростью, образуется волна, и скорость распространения этих волн становится безвредной. Если указана энергия волны на единицу длины, то она получает дополнительную энергию волны в секунду (поскольку корабль перемещает единицу длины за единицу времени).
Но часть этой энергии его несет ранее сформированная волна. То есть волна Эйна переносит количество энергии в единицу времени на каждую плоскость. Остальная энергия засчет других источников энергии, в данном случае, за счет энергии судна.
- Поэтому корабль выполняет свою работу за каждую единицу времени и приступает к формированию волн. А так как движение корабля в единицу времени равно, то сопротивление испытанию определяется по формуле.
- Это значит. Рассмотрим проблему волнового сопротивления более подробно.
Мы думаем, что жидкость однородна, несжимаема, идеальна и везде получает только гравитацию, и что движение жидкости не имеет вихрей. Людмила Фирмаль
При этих предположениях силовая волна, возникающая при движении тела горизонтально с постоянной скоростью под свободной поверхностью жидкости, определяет сопротивление, которое получает тело, которое называется воздухом горного хребта. Этот случай ограничивается изучением плоских задач и бесконечно глубокой жидкости.
В этом случае очень удобно использовать комплексные переменные. Поэтому рекомендуется немного изменить предыдущую нотацию. То есть она обозначается горизонтальной осью координат, которая лежит на свободной поверхности жидкости в равновесии, и восходящей вертикальной осью.
- Мы также вводим комплексные переменные интегрированный потенциал скорости. Прежде всего, решается задача о вынужденных волнах, возникающих при движении вихрей интенсивности, которые расположены на глубине ниже свободной поверхности жидкости и движутся с постоянной скоростью параллельно положительной.
- Удобнее рассматривать установившееся движение, полученное при наложении на ход предыдущего равномерного обучения в направлении скорости отрицательной оси.
Если мы покажем возможность этого устойчивого движения, то: В этом стационарном движении свободная граница жидкости действует как линия потока, так и постоянное давление. Формула Бернулли для давления. Замените выражение здесь Легко получить.
Поскольку генерируемая волна очень мала, мы считаем, что квадрат компоненты скорости предыдущего уравнения можно игнорировать на линии. Людмила Фирмаль
Затем она принимает форму указывая постоянную давления на линии, мы предполагаем, что перед вихрем, то есть жидкость не возбуждается, то есть величина стремится к нулю. Является уравнением свободной границы жидкости. И это понятно из равенства.
Следовательно, равенство в свободной линии учитывая малую величину, можно предположить, что это равенство заполняется на оси. Получено граничное условие. Получите условие, выразив, что линия является линией потока устойчивого движения. Или. Заменив правую часть этого уравнения, это можно сделать для малых, достигающих граничного условия.
За исключением величин, для определяемой функции выполняются следующие граничные условия. Для простоты приведу обозначения. Если ввести символ а в действительную часть комплексного числа и мнимую часть этого числа, то получим.
Поэтому условие пишется в сложной форме. Это условие, в частности, означает следующее. Как упоминалось ранее, функции, как правило, являются модульными и. Кроме того, очевидное в частном случае вихревого движения, которое мы сейчас рассматриваем, функция должна быть регулярной по всей полуплоскости, за исключением точки, где расположен вихрь.
Сделайте это точкой с координатами. Вблизи этой точки, функция должна иметь следующий вид Где-регуляризованная функция окрестности точки. Получил представление о функциях Мы формируем здесь функцию. Эта функция не является сингулярной по всей полуплоскости, за исключением того, что она находится рядом.
Где регуляризованная функция окрестности точки. В зависимости от условия функция принимает действительные значения на действительной оси независимой переменной. Однако, учитывая полуплоскость, эта функция может быть продолжена аналитически до верхней полуплоскости в соответствии с принципом симметрии Шварца.
То есть значение функции в точках, которая симметрична относительно оси, должно быть комплексно сопряженным, поэтому она должна принимать следующее. Это создает уже аналитическую функцию на всей плоскости комплексной переменной. Эта функция имеет особенность в точке, определенной.
Кроме того, в этом пункте есть своя специфика. Это связано с тем, что из Формулы выведено, что рядом с этой точкой находится выражение. Указывает, что точка является полюсом функции. В этой функции нет других особенностей на конечном расстоянии.
Если предположить, что эта функция регулярна вблизи точки бесконечности и исчезает, то получается следующее уравнение: Общие решения однородных уравнений. Применяя обычный метод вариации любой константы для решения неоднородного уравнения, рассмотрим функции и придем к следующим уравнениям для их определения.
Учитывая функцию, которая стремится к нулю, легко показать с символом, когда точка бесконечна в направлении положительной вещественной оси. Однако интеграция по частям обеспечивает выражение.. Поэтому после очень простого расчета найдите следующую формулу для определения комплексного потенциала.
Нетрудно заметить, что выражение этого сложного потенциала отвечает всем требованиям. Больше ничего. Не существует решения проблемы, которое удовлетворяет всем требованиям. фактически, мы предполагаем, что есть и другое решение проблемы.
Формирование разницы. Функция должна иметь следующую форму рядом с точкой, например: Функция должна быть регуляризованной функцией в нижней полуплоскости. И вы должны выполнить условия. Поэтому функция Его можно аналитически продолжить до верхней полуплоскости по принципу симметрии Шварца.
Таким образом, вся плоскость регулярна, то есть. Вся нижняя полуплоскость ограничена. Позволять Значение Сказать мне больше. С этого момента Неравенство продолжается Таким образом, существует оценка Эта оценка доказана только для точек в нижней полуплоскости. Но поскольку функция принимает комплексно сопряженное значение в точке, симметричной относительно действительной оси, это.
Оценка проводится по всей плоскости. Но тогда из неравенства кошма мы видим, что существует линейная функция, где действительное число из-за условия. Если вы консолидируете это равенство, вы можете увидеть следующее: И потому что условия, как правило, должен быть равен нулю. Для вдоль положительной вещественной оси сумма должна быть равна нулю, поэтому.
Докажите вышеизложенное утверждение . Теперь определите форму свободной поверхности. To сделайте это, используйте равенство. Если вы различаете равенство, вы можете увидеть следующее: помощью этой формулы, предполагая, что материальная часть отделена, вы можете легко очевидно. Так, на большом расстоянии перед вихрем свободная поверхность жидкости должна приближаться горизонтально.
Еще одна фотография сделана в дальнем конце вихря. Во-первых, существует равенство фактически интеграл слева, взятый вдоль всей материальной оси, может быть дополнен интегралом, взятым над полукругом бесконечно большого радиуса, расположенным в верхней полуплоскости. Но в верхней полуплоскости есть только один полюс функции под знаком интеграла.
Найдите остаток функции в этой точке и умножьте его, и вы получите интегральное значение. Мы можем написать. Поэтому мы также можем написать. Исходя из этого, получаем следующее выражение. Это, по-видимому, и есть длина опережающей волны, которая распространяется со скоростью вдоль поверхности бесконечно глубокой жидкости.
Мы также вычисляем силы, действующие на вихри .Если проекция этой силы на ось представлена каждой из них, то формула известного Чаплина выглядит следующим образом. Здесь интеграл имеет место в произвольном замкнутом контуре, который окружает вихрь . Используя выражение, напишите следующее.
Очевидно, что в нижней полуплоскости существует регуляризованная функция. Таким образом, функция, которая играет функцию точка, в которой находится вихрь. И по теореме остатка мы получаем. Введите выражение для последнего интеграла вместо новой переменной Вы можете это запомнить.
Следует подчеркнуть, что в плоскости интеграционный путь полностью находится в нижней полуплоскости, а в плоскости он также находится в верхней полуплоскости. Функция Интеграл называется экспоненциальной функцией. Если она положительна и путь интегрирования находится в верхней полуплоскости, то интегрирование может быть получено вдоль действительной оси.
Обойдите точку сверху бесконечным полукругом. Так как остаток подынтегрального выражения в этой точке равен, то интегральные значения над полукругом равны. Таким образом, мнимые части равны-кроме того, введем обозначение и тогда мы становимся равными.
Предположим, что путь интегрирования находится в верхней полуплоскости. Так мы становимся равными. Если мы разделим действительную и мнимую части в этом уравнении и подставим вместо них их значения, мы получим окончательное выражение. Первое из этих уравнений определяет импеданс. Она также может быть определена по общей формуле, представленной в начале этого раздела.
Подставьте его значение вместо амплитуды генерируемой волны Из этого последнего уравнения мы можем видеть, что амплитуда волны и импеданс волны уменьшаются в соответствии с экспоненциальной функцией. Закон увеличения глубины погружения. Для зависимости волнового сопротивления от скорости вихря простые исследования показали, что при очень низких и очень высоких скоростях волновое сопротивление очень мало.
Достигните максимального значения в уравнение показывает, что вихревой подъем состоит из частей. Жуковский — это лифт и дополнительный лифт. Он имеет положительный знак на низкой скорости c и быстрый и отрицательный. Аналогично решается задача о вынужденных волнах, возникающих при движении источника силы.
Поэтому мы приводим только конечное выражение. Интеграционный потенциал в данном случае имеет следующие значения. Для комплексной скорости, получим формулу профиль волны определяется уравнением больше почти равный. Амплитуда волн, которые образуются.
Составляющая силы, действующей на источник, определяется по формуле. Первая из этих формул указывает на то, что тянущая сила действует на источник, что также происходит при неограниченном потоке. Кроме того, волновое сопротивление также может быть представлено амплитудой генерируемой волны, согласно общей формуле, приведенной в начале этого пункта.
Подъемная сила совпадает с формулой для дополнительной подъемной силы, полученной в случае. Остается только заменить его этой формулой. Обратите внимание на следующее. Если вы берете правую часть выражения, которое дает комплексное выражение скорости для исходного случая, для выражения для нового комплексного потенциала.
Как вы можете легко убедиться, он отвечает всем вышеперечисленным требованиям. Очевидно, что существует диполь с моментом в направлении вдоль оси, поэтому предыдущая формула определяет, какая волна возбуждается, когда диполь движется под свободной поверхностью жидкости. Аналогично можно определить движение, соответствующее диполю с моментом вдоль оси или в любом направлении, и движение, соответствующее элементу более высокого порядка.
Комбинируя такие движения, нетрудно получить волну, которая возбуждается при движении параллельно оси круга с радиусом, центр которого находится в точке. Дело в том, что комплексный кинетический потенциал неограниченной жидкости является в данном случае формулой. Это упражнение показывает, что его можно рассматривать как суперпозицию потоков.
Генерируется из диполя с моментом в направлении вдоль оси, а другой генерируется из вихря интенсивности. Введите формулу и добавьте полученный потенциал и потенциал для достижения желаемой формулы амплитуда волн, генерируемых далеко позади тела, определяется по формуле.
Для сопротивления и подъема волны, вы получите следующую формулу. Последний член формулы — подъемная сила Архимеда. Предполагая, что вы достигнете формулы вихревого случая. Если вы это сделаете, подставьте значение. Волновое сопротивление быстро уменьшается с увеличением.
На определенной глубине импеданс волны очень мал, очень быстр и мал, достигая своего максимального значения. Рассмотрим волну, возбуждаемую движением любого контура параллельно оси с постоянной скоростью. Сделайте предварительное замечание ниже. Суммируя оба рассмотренных выше потока, получаем волны, возбуждаемые вихревым источником.
Подумайте о последнем, как о каком-то моменте. Вы получаете следующую формулу. Для волн, образующихся далеко позади вихревого источника, добавьте уравнение, которое необходимо заменить, и уравнение. Здесь комплексный потенциал используется для описания скорости потока, которая получается, когда контур движется в неограниченном пространстве.
В этом случае существует регулярная функция в области вне контурной линии, и по формуле Коши получается равенство. Существует переменная точка контура, и контур работает в положительном. Можно предположить, что движение жидкости происходит за счет наличия большого количества вихревых источников в контуре С, кроме того, видно, что вихри и источники расположены в элементах.
Но тогда, если заменить уравнение и выполнить интеграл по контуру, то получится волновое движение, вызванное указанным выше распределением вихревого источника. Это волновое движение можно считать первым приближением к тому, что вызвано движением. Дело в том, что из-за наличия свободных поверхностей происходит незначительное изменение значений вихрей и источников, расположенных на контуре.
Это изменение, очевидно, будет меньше, поскольку контур глубже. Поэтому рассматриваемое приближение лучше при большей степени погружения контура. Итак, в первом приближении находим выражение. Узнайте о профиле волны, который формируется далеко позади тела, используя формулу.
Итак, амплитуда генерируемой волны имеет следующую формулу. И используя формулу, приведенную в начале этого раздела, на волновом сопротивлении мы нашли. Давайте рассмотрим примера. Пусть контур представляет собой окружность с радиусом, центр которой находится в глубине, а скорости циркуляции по контурной линии имеют заданное значение.
Есть формула для движения цилиндра в бесконечном потоке. Таким образом, используя формулу, можно увидеть следующее. Если вы развернете подынтегральное выражение в ряд Лорана вблизи точки, вы можете легко увидеть, что. Таким образом, по теореме остатка.
Таким образом, амплитуда генерируемой волны является значительным. Для волнового сопротивления, получим следующую формулу. Обе эти формулы согласуются с приведенными выше формулами. В качестве второго примера рассмотрим случай, когда контур представляет собой эллипс, его центром является глубина, а ось ориентирована параллельно осям.
Для простоты предполагается, что величина тиража равна. В этом случае обтекание контура с бесконечным потоком жидкости определяется с помощью вспомогательных переменных и формул Выполняет полученную замену.
Но из теории функции Бесселя. Для этого используя формулу. Если вы получаете вышеуказанное значение. Поэтому амплитуда волны, возбуждаемой движением эллипса, значительна. Для волнового сопротивления, формула.

