Установление связи между адиабатическим и изотермическим модулями упругости и скоростью звука.

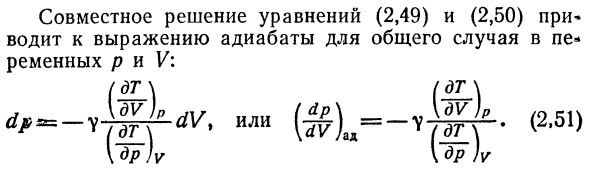
Установление связи между адиабатическим и изотермическим модулями упругости и скоростью звука.

• Установление связи между Теплоизоляция и изотермические Модуль и скорость Во-первых, мы получаем уравнение adi.* Редукция в общем случае, основанная на Формуле B, 16）* И Б, 17). Потому что рассматривается процесс теплоизоляции、 d’q = Q и уравнение BD6) можно записать следующим образом: =0.Б, 48.） Из уравнений B, 17) и B, 48) можно получить уравнения Уравнение теплоизоляции в общем случае выражается следующим образом Независимые переменные T и V： Б, 49） Когда модуль упругости связан с изменением* p и V, найти адиабатическое уравнение в том же Переменная.

Из уравнения состояния T = f (p, V) определим производную Разница температур： Совместное решение уравнений B, 49)и B, 50) приводит к представлению адиабата в общем случае ne Пояса P и V： Или По определению, теплоизоляция и изотермичность Модуль упругости： Для изотермического процесса (dT-O)、 Выражение B, 50) можно записать в виде: \ ду) п (ДП\, 9″ Н 7ET-S1B> 53） Е ДП) в Сравните последнее уравнение с уравнением B 51）、 Мы это выясним： Или, согласно соотношению B, 52： Б, 55） Учитывая, что обратная упругость является коэффициентом Степень сжатия： Счастливый= » ^ 7; аренда= — K ^ ’ Получаем зависимость следующих коэффициентов Степень сжатия： V = fe’B. пятьдесят семь). Определена скорость распространения звука в окружающей среде Уравнение Ди =-??- От, Р-плотность среды.

Альтернативное значение B, 57) скорость звука B, 61) выражение, наконец Получите желаемое соотношение. Людмила Фирмаль

Плотность среды обратно пропорциональна Удельный объем p^ -, то В. пятьдесят восемь） Распространение звука в среде Адиабатично Поэтому процесс^ Вт <2-59） Пятьдесят девять Заменить выражение Я доктор \ * В выражении скорости звука получается уравнение. ^ ^ «Сжечь BD）） Или по соотношению Б 57）： Наконец, вы можете установить соединение между модулями Звуковая эластичность и скорость.

От Лиз А D задачи и упражнения 1.Напишите выражение начала первого В случае единичного объема непроводящих диэлектриков、 Помещенный в постоянное равномерное электроэнергии вне Электрическое поле (например, между обкладками конденсатора）、 Для простоты предположим, что векторы E и D параллельны. Параллельна в каждой точке, и определенный объем постоянен. Решение. Элементарный электрический Работа единицы объема диэлектрика — Р ^ — EdD. By состояние, пренебречь работой по расширению Расширения (сжатия) ПДВ, описать в следующем виде: d’Q ЛН 4л ’ Где d’q-основное количество подводимого тепла. Uuom-энергия системы, в том числе энергия Электрическое поле. — > Введем электрическую поляризацию P ->->-> D = E + 4nP и извлечь и установить энергию электрического поля в вакууме из уравнения полной энергии Тогда вы получите d’Q-dU-EdP.

• 2.Рассчитайте работу, выполненную снаружи Внешнее электрическое поле при поляризации диэлектрика. Solution. As термодинамика Система принимает 2-в-одном диэлектрике Плоская пластина конденсатора. Работа Это необходимо выполнять при передаче зарядов Dq между 2 точками с Потенциометрическим q> d’w = — равно ydq. Если S-площадь пластины, а A-поверхность Итак, плотность заряда, а затем заряд q=.By Из-за электрической индукции? =4π0, изменение Электрическая величина dq = Sdo = S-j -. Потенциал и электричество Поле связано соотношением φ= 7 7, тогда φ и И DQ в выражение работы Д ’западной долготы выглядит так: д’ западной долготы-Джей-Эдд. Единичный Объем 1 * ^ = 5 / работа, связанная с диэлектриками Диэлектрик, равный： С И затем… 〜 Где P-вектор поляризации единичного объема диэлектрика Диэлектрический. 

3.Вычислить работу испарения воды、 1 заплесневелая вода А8 г) переход на следующий пар 100°C увеличение объема VB-VA == = 30,186 СМГ / моль. Давление во время процесса постоянно Во все времена Р = 1,013-10е сутки / см2 = 1 атм. Повторите W = = 3,06 кДж. 4.Дано 1 моль газа при нормальных условиях Вычислите условие (Va = Vo = 22414 cmz,/ 7 = 1 атм) Работы, необходимые для уменьшения количества этого газа Шестьдесят один 2 раза, учитывая, что процесс следует за мальчиком Ла Мариотта： Повторите 1 ^^-1.57 кДж. 5. 200 г воды, калориметр (Начальная температура / i = 20°C), медленный кусок 300 г металла по массе, начальная температура ？2 = 10°С равновесная температура равна： Алюминий (^=27,0 г) 39,5°С, железо (Р,= 55,8 г） 31.9°C, для цинка (ja = 65.4 g) 29.8°C, для серебра (p,= = 107,9 г) 26,2°С. найти удельные (пробные) и коренные зубы Удельная теплоемкость этих 4 металлов © (C-атом Вес.) Повторять Для алюминия: пальто= 0.21 кал / г * град. C = = 5,67 кал / град; Для железа: buzz= 0.116 кал / г-град; C = 6.47 кал / виселица; Для цинка: SUA = 0.093 кал * град; C 6.08 кал / град; Для серебра: sua = 0.056 кал / г * град; » 6.04 кал \град. 

Здесь мы устанавливаем связь с соотношением теплоты* Вода Кость-и скорость звука в окружающей среде. Людмила Фирмаль

6.Длина штанги / протягиванный размер- Loi R. предполагая, что деформация является упругой(если длина равна Стержень является функцией P и температуры), показать Изотермические и адиабатические коэффициенты Расширение y-gp соединено » отношением дл КТ(дл ’ДПЛ-Т ^ ВДП Где ci и cP — теплоемкость стержня при определенной длине. Длина и постоянное натяжение соответственно. Решение.

Работа упругой силы стержня когда дл растягивается только-начало первого, потому что оно равно ПДУ Термодинамика принимает вид: d’q = dE-PdU, где Å -. Энергия стержня. Напишите равенство B, 12}в изменении* В n/, T и переменной P, T введем обозначения ＃） Шестьдесят два Итак, по определению cg и cp： Уравнение B, 12) переменная P,/, semi- Чай с отношением B, 63）： Для процесса изоляции, d’q = 0, whice * Л \ — \ ДРП-(СЛ дл \ [Ил телефон DPH〜 ’ * л \ — \ ДП）{ dt 

7.Определите изотермическую операцию* Расширение газа по Вану Дейр Уарзазат. Решение. Выражена работа по расширению газа Он представлен интегралом： Два Я Уравнение ван-дер-Ваальса A, 9), как решенное Для давления P, формат _ РТ_ П-в-б П2＃ Поэтому он работает с изотермическим расширением ван дер * расширение газа на 1 моль по формуле Вальса равна следующему： Vi и V2-начальные и конечные значения молярных зубов Объем. Шестьдесят три

8.Определите следующие особенности Тропический процесс： ПВ° С то = const; ПВЛ> 3 = const и; pVlf5 = const и Коэффициент y равен 1,4. Решение. Процесс p U0 * 8 = const принадлежит Относится к первой группе политропных процессов. н <В. Коэффициент а= _ =-= ^ 5 ^-^ = ^。 В этом процессе газ* Жара найдена, и 3 из своих 1 минут увеличены Увеличение внутренней энергии газа, а через 3 минуты 2-полностью Груз внешних работ. Следовательно, температура Во время расширения в этом процессе газ увеличивается. 9.In точно так же Показывать положение относительно других процессов / ?Положение политроп на диаграмме Y. 10.In политропный процесс, газ в гонке* Распространение подвергается 10 ккал тепла.

Вычислить процесс Объем газа увеличивается в 10 раз, давление увеличивается Он уменьшается в 8 раз. Повторите n = 0.9; a== -^ -; W ’= 2 ккал. 11.Оно совершено в процессе сжатия Из газа отводится 20 000 кг работы и 60 ккал тепла. определите n и посчитайте-y-L D. Повторите n = 0.9. 12.По существу это показать Справедливо, в соответствии с законами каждого государства В этих отношениях У2 Шестьдесят четыре Где Yi и Y2-коэффициенты удельной теплоемкости〜 Вещество RaD1 и raDz — это адиабатические коэффициенты сжатия. Сжимаемость материала РСЧ и рк2 ″» значительное давление.

Решение. Используйте ранее полученные Найдите соотношение B, 57) и A, 24). Откуда Вл У2 радиоуправляемый Последнее уравнение может быть успешно применено Брак Вещества, подпадающие под определение и закон резюме Если вы готовы узнать из опыта, вы несете ответственность государства Коэффициент теплоемкости не менее 1 вещества、 Соблюдайте этот закон.

Смотрите также:

Решение задач по термодинамике

Адиабатический процесс.	Круговые процессы, или циклы. Цикл Карно. Идеальные циклы тепловых двигателей. Круговые процессы.
Политропический процесс.	Прямые и обратные циклы.