Оглавление:



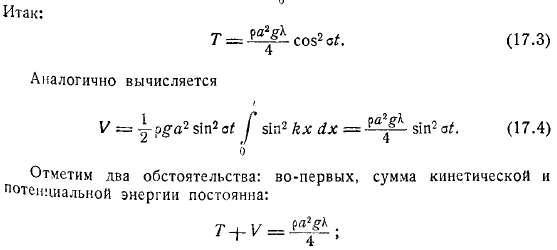

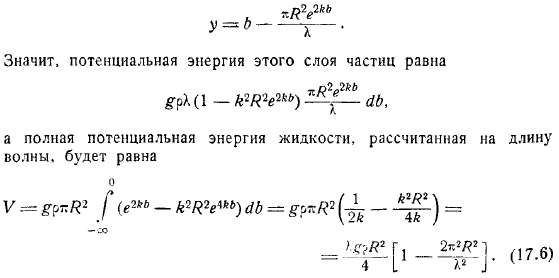
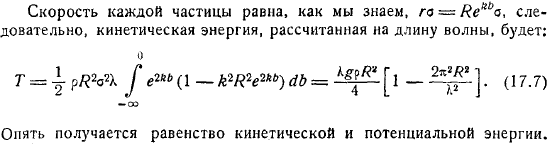

Энергия волн
В этом разделе гидромеханики мы рассмотрим, из каких частей состоит энергия волны и как она передается от одной части жидкости к другой. Сначала рассмотрим волны несжимаемой жидкости, возникающие под действием силы тяжести. Здесь энергия волны складывается из кинетической энергии движения.
От потенциальной энергии связано с тем, что отдельные частицы жидкости и центр тяжести жидкости в волне выше равновесного состояния. Во-первых, рассмотрим невращающуюся периодическую длину волны жидкости на конечной глубине (если вы получаете бесконечно глубокий случай жидкости). В этом деле трохоидальных волн следовательно, жизненная сила на длину.
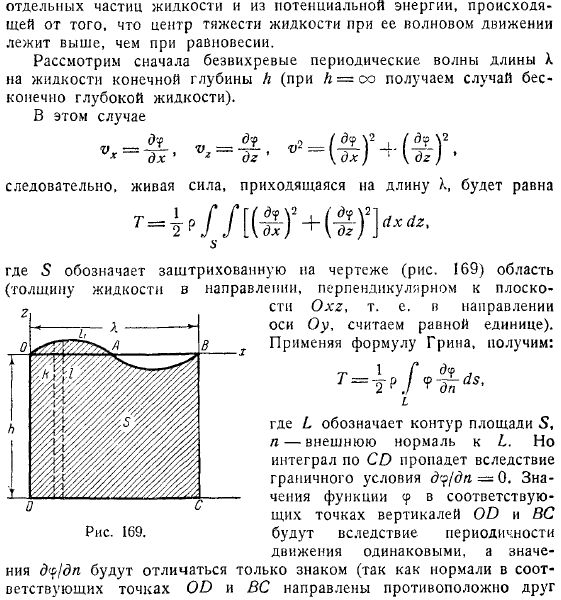
- Здесь обозначим заштрихованные участки на чертеже (предполагается, что толщина жидкости в направлении оси, то есть перпендикулярно плоскости, равна).
- Используя зеленую формулу, вы можете сделать следующее. Здесь контур области показывает внешнюю нормаль, но условия интегрирования исчезают из-за граничных условий.
Значение функции в соответствующей вертикальной точке обусловлено периодичностью. Людмила Фирмаль
Движение одно и то же, значения различаются только по знаку (так как нормали соответствующих точек обращены друг к другу в противоположных направлениях). Наконец, направление оси можно рассматривать как направление внешней нормали, но может быть.
Потенциальная энергия на длину. Я рассчитал его следующим образом: нарисуйте вертикальные плоскости. Давайте определим точки на оси, а затем. Тогда потенциальная энергия тяготения равна (по известной формуле), потому что над осью находится объем жидкости, и масса этого объема, а центр тяжести находится на высоте.
- Другими словами, потенциальная энергия на длину выглядит следующим образом . Так, например, для стоячих волн на жидкости конечной глубины.
- Итак, если вы сделаете расчет, он выглядит так. Он рассчитывается таким же образом Обратите внимание на ситуации.
Во-первых, сумма кинетической энергии и позиционной энергии постоянна. Во-вторых, кинетическая и потенциальная энергии всегда идут друг к другу, а их средние значения, взятые за период, равный периоду, одинаковы. В случае прогрессивной волны.
А расчет похожий на только что данный дает. Людмила Фирмаль
Поэтому и кинетическая энергия, и потенциальная энергия здесь остаются постоянными. В случае трохоидальной волны позиционная энергия может быть рассчитана таким же образом. Но мы предпринимаем перенос энергии разные действия.
То есть мы учитываем соседних трохоида, которые соответствуют значениям. Огороженная ими площадь и вертикальные линии на расстоянии друг от друга будут равны. Конечно, центр тяжести частиц, составляющих эту область, находится на прямой линии. Это происходит потому, что любая частица выше этого уровня соответствует той же частице ниже.
В состоянии равновесия эти частицы находятся на прямой линии. Следовательно, потенциальная энергия этого слоя частиц. И суммарная потенциальная энергия жидкости, рассчитанная на длине волны. Поскольку скорости каждой частицы равны, как известно, кинетическая энергия, рассчитанная для длины волны, равна. Опять же, получено равенство кинетической и позиционной энергий.

