Оглавление:


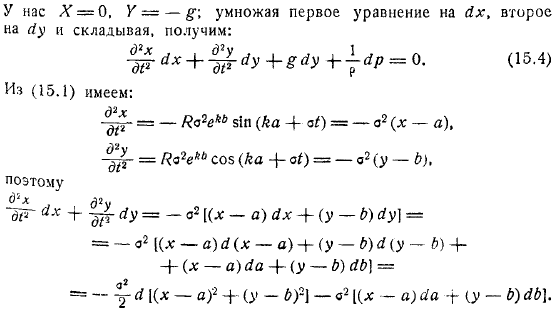

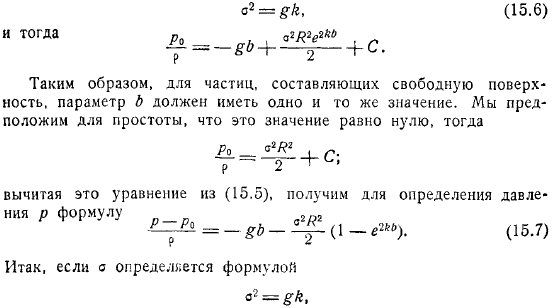


Трохоидальные волны Герстнера
Случай круговых орбит отдельных частиц в волнах конечной амплитуды рассматривался гельстнером и Рэнкином. Из вышесказанного следует, что рассмотренные ими движения гидромеханики не были. В начале этой главы идеальное волновое движение жидкости за счет потенциальной силы является вихревым.
Для решения рассматриваемой задачи применим переменную Ла-гранжа. Расположите ось горизонтально, а ось вертикально вверх. Лагранжева координата частицы конечной амплитуды , то есть параметр, отличающий одну частицу от другой. Что мы можем различать по поверхности.
- Таким образом, мы получаем с другой стороны, если они это сделают, они будут сопряженной функцией в. Конец это нелинейное условие обычно принимается при исследовании волн конечной амплитуды при отсутствии вихрей.
- Они предлагают подумать о движении, в котором координаты частицы с параметрами будут находиться в этот момент.
Проверьте, выполняется ли основное уравнение движения. Людмила Фирмаль
Тогда вам нужно выполнить еще одно граничное условие. Давление на свободную поверхность должно быть равно определенной величине (атмосферному давлению).
Во-первых, выполняется уравнение непрерывности. Потому что не зависит от времени, это непрерывное уравнение, выраженное в форме Лагранжа. Проверьте основное уравнение движения. Если мы умножим первое уравнение, а затем умножим и сложим, то получим.
- Таким образом, вы можете интегрировать уравнения. Если вы вставите значение y здесь, это в конечном итоге будет выглядеть так. Равенство выполняется при замене найденного значения.
- На свободной поверхности жидкости давление всегда должно быть постоянным. Поскольку время вводится только через косинус, коэффициент должен быть равен нулю.
Таким образом, для частиц трохоидальных волн, составляющих свободную поверхность. Параметры должны иметь одинаковое значение. Для простоты это значение принимается равным нулю. Вычитая это уравнение из, вы получаете уравнение для определения давления.
Затем формула определяет волновое движение, удовлетворяющее как точному дифференциальному уравнению, так и условию свободной поверхности. Людмила Фирмаль

