Оглавление:







Ламинарный поток, параллельный плоской пластине
- Поток жидкости на плоской пластине имеет гидродинамический пограничный слой, в котором скорость жидкости изменяется от нуля до скорости ядра на поверхности пластины. Течение на границе пограничного слоя. При массопереносе между жидкостью и пластиной также образуется диффузионный пограничный слой, концентрация растворенного в нем вещества равна. Вещества изменяются от равновесного значения границы с твердым веществом до концентрации, равной концентрации в stream. Это похоже на температуру и гидродинамику. Пограничные слои часто имеют разную толщину в одной и той же системе, диффузионные и гидродинамические пограничные слои. Она может быть разной.
Практика, тепло-и массообмен часто происходят в пределах одной и той же системы, 3 различных пограничных слоя существуют одновременно, и все они являются Они могут иметь разную толщину. Если движение ламинарное, то массоперенос в направлении, перпендикулярном движению жидкости, происходит только в результате молекулярной диффузии и связанной с ней конвекции Поток, рассматриваемый в гл. 32.Дифференциальное уравнение баланса масс многокомпонентных систем, в которых происходит диффузия, имеет вид ч. 9.Если Уравнение устойчивого двумерного течения бинарной смеси постоянной плотности(9.
Основная задача конвективного теплообмена довольно сложная, и решение ее зависит от нескольких переменных. Людмила Фирмаль
Если источник компонента А отсутствует, а диффузия в направлении х игнорируется, то уравнение (34.1) принимает вид: (34.2) Это уравнение аналогично упрощенной форме дифференциального уравнения для импульса двумерного потока жидкости с постоянной плотностью и вязкостью. М-3 Решение последнего уравнения графически показано на рисунке. 12.Безразмерная 8-в виде зависящей от скорости(обычно обозначается через X). Если коэффициент диффузии равен Rdv и кинематика V равно, и уравнения (34.2) и (34.3) идентичны, за исключением зависимой переменной и.
Последний может быть заменен на безразмерный с дифференциальным уравнением Используйте-и-как эти новые переменные, чтобы установить значения так, чтобы граничные условия были похожи. Отель расположен в самом центре города. «Наружный диаметр.- Южная Дакота、 9d и SDO на пластине и в потоке считаются постоянными, соответственно. Граничные условия движения в пограничном слое на плоской пластине при диффузии из плоской пластины в потоке Ниже: если y = 0 Таким образом, в данном конкретном случае решение уравнения диффузии и импульса будет идентичным.
Поэтому профиль безразмерной концентрации и Поскольку скорость пограничного слоя одинакова, толщина диффузионного слоя и гидродинамического пограничного слоя одинаковы. Важно, что 1 из требований, которые приводят к тому же решению выше, является эквивалентностью OAB и V. фактор-это безразмерный комплекс, известный как число. Шмидта и равняется единству рассматриваемого конкретного случая. Числа Шмидта не только показывают связь между транспортом и импульсом、 Тепло и импульс. Помните, что в разделе 24 уравнение теплового равновесия сравнивалось тождественно с числом Прандтля, которое равно 1. Уравнения (34.2) и (34.3) Формула (24. 1) аналогично.
Приведенные выше граничные условия можно сравнить с 309 страницами данных. Как уже указывалось, решение уравнения (34.3) показано графически на рисунке. 12. 8.Эта иллюстрация справедлива для уравнения с числом Шмидта, равным 1 (34.2、 Только когда скорость диффузии приближается к нулю. Это решение показано на рисунке 12.8, скорость Он перпендикулярен пластине ai и равен нулю. Если диффузия от пластины к потоку происходит в установившемся состоянии, то составляющая скорости u не может быть равна нулю на поверхности. Когда yn приближается к нулю, рисунок 12.8 может быть применен к массопереносу только в пластинчатых и ограниченных случаях.
Решения уравнений (34.2) и (34.3), если оно не равно нулю на плоскости, находят путем преобразования уравнения в частных производных в нормальную производную. Типы, использующие аналогичные преобразования(12. 68) и (12. 69) уравнение:___________________ В результате уравнение (34.2) имеет вид*( \ съедено » — Оло и 5С./(с.) \ л.- ел. Я-сука. Л] 22 Аналогичная формула(24. Три)、 В граничном условии, если y = 0 (q = 0), было задано условие•p A * _ с A = 0 Yke. Формула (12. 72)как вы можете видеть, требование равняться нулю= 0.To ваши 12 и 24 «、 Формула (12. 73) / (m)) привело требование, которое равно нулю.
С этим случай f (n)= — — — c) равен нулю, поэтому f (n) Следовательно, это должно быть постоянное значение.»Вам нужно изменить применение преобразования, чтобы быть правильным Умный. если y = oo, как показано, — = 1.0.С Фр. Если = 1.0, то выражение(12. 72) до = 1,0.Дебаты Приведенные выше граничные условия суммируются следующим образом: если y = 0: (Веха), / = сцепка; г = ОО ЕА-0л₌Р Ты можешь его съесть. ^ / в) эль.- элед₈-оло В Первое граничное условие, константа, содержит фактор −2.Скорость поверхности зависит от соотношения (34.5) Эккерт и Дрейк 142] показали, что атомные условия достигаются при постоянной температуре и концентрации вблизи стенки.
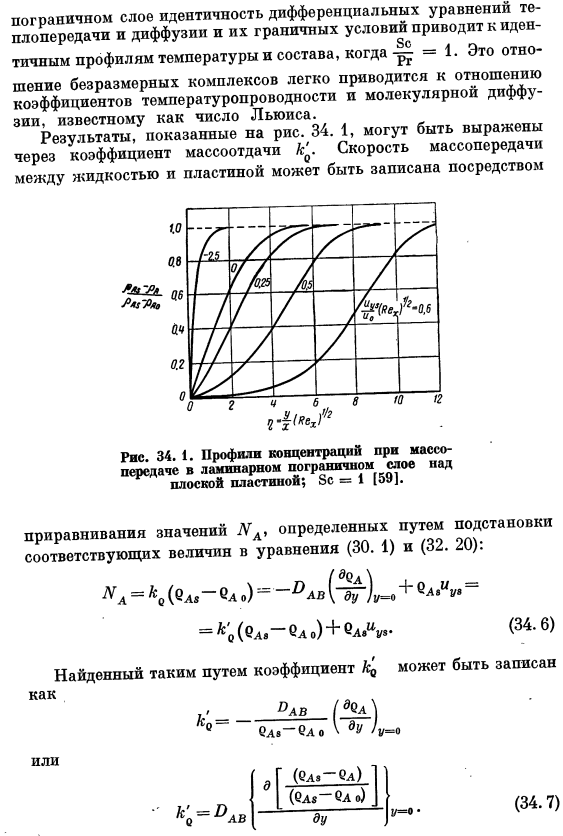
Иллюстрация уравнения (34.4) показана на рисунке. 34. 1 представляет собой 2-компонентную смесь жидкостей с числом Шмитта 1.Отображаются как положительные, так и отрицательные значения. Значения параметров (вехи),/*; положительный относится к массопереносу от пластины к жидкости, отрицательный относится к массопереносу в противоположном направлении. Кривая Параметр равен нулю и относится к системе, в которой скорость массопереноса пренебрежимо мала по сравнению со скоростью свободного потока. Эта кривая совпадает с безразмерным профилем. Рисунок 12. 8.It это также совпадает с кривой Pr = 8 на рисунке 1. 24.
- Одновременное движение тепла и вещества во время движения. Истинная идентичность пограничного слоя, дифференциального уравнения теплопередачи и диффузии, а также их граничных условий дают одинаковый температурный профиль и профиль состава для случая= 1. Безразмерный комплекс можно легко свести к соотношению термической и молекулярной диффузии, известному как диффузионное число Льюиса. Результаты показаны на рисунке. 34. 1 может быть представлен коэффициентом массопереноса k’.Скорость массопереноса между жидкостью и пластиной. Уравнение 30.
Коэффициент k₀, полученный этим методом Я могу это записать. (34.7) Некоторые особые случаи, подлежащие рассмотрению связь между компакт-диском и компакт-диском разделена на части. 38. Сравнивая формулы (34.7) с кривой на рисунке 3, можно сделать качественный вывод о характере изменения коэффициента массопередачи. 34. 1.Система, к которой применяется параметр («Не»)*отрицательный (массоперенос от жидкости к пластине), большой угол наклона (y = 0, 1] = 0) в начале координат, соответствующий высокому коэффициенту. Массоперенос.
Граничные условия могут быть заданы распределением температур на поверхности либо (плотностью теплового потока в любой точке поверхности. Людмила Фирмаль
Для систем с большим положительным значением этого параметра(массоперенос от пластины к жидкости) наклон кривой в начале координат уменьшается、 Указывает на значительно более низкий коэффициент массопереноса. Измеряя наклон в начале соответствующей кривой на рис. 8, можно вычислить численное значение локального коэффициента массопереноса жидкости при 8С = 1. 34.1 и Примените формулу (34.7)для расчета A^.Для предела= 0, CD =k₀ = градиент в начале координат равен 0.33.So .
Подставляя эту формулу в Формулу (34.7), получаем следующую формулу: d ^ — = 0,33 (да) (34.8) Если 8c-это жидкость, отличная от единицы, Рисунок 3 34. 1 — Формула(34. 4) Вы можете получить, решая. уу= 0 24. 1 применяется к массопереносу, если ордината берется для pCA * _ ^ A>и параметр Pr получается за 8 секунд. Для коэффициента массопереноса получена следующая приближенная формула: Соответствует рисунку профиль концентрации 24.1: — ^=0.33 (веха) /’(8С) / *.
Безразмерный комплекс-известный как число Шервуда, соответствует числу нуссельта теплопередачи. Уравнение (34. 9) методологии и допущения, сделанные при разработке методологии и Допущение анализа теплопередачи в секундах. 24, светодиодные (34.10)) Формула (24. 8) до. Как и выражение (24.8), выражение (34.9) применяется к 8c> 0.6.In кроме того, обе формулы применимы только в том случае, если-малые значения.
Средний коэффициент массопереноса пластипа конечной длины описывается уравнением (34.9)со значением ad для бесконечно малых поверхностных элементов.、 Интегрируйте по всей длине пластины. Этот прием показан в гл. Определите средний коэффициент теплопередачи плоской пластины на основе 24 локальных факторов. При рассмотрении теплопередачи формула для среднего коэффициента отличается формулой для локального коэффициента и коэффициентом 2.Таким образом, получаем следующую формулу: Среднее соотношение 8bm = 0.66 (Бэб) ’/’(8С),/’、 Где среднее число Шервуда содержит средний коэффициент массопереноса пластины длины b.
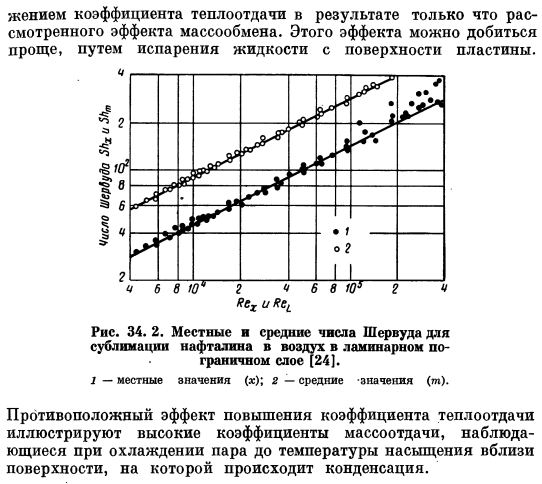
В отличие от многих исследований теплопередачи, существует мало сообщений об экспериментальных исследованиях массопереноса из плоского тела. plate. In недавняя статья Кристиан и Кезиос [24]описывают измерения локальных и средних коэффициентов нафталина, которые сублимируются в воздушный поток, протекающий параллельно оси полого цилиндра. Их Результат показан на рисунке. 34.2.Линии, проведенные вдоль экспериментальных точек, определяются по формуле (34. 9) и 34.
Коэффициенты различаются только выраженными в Формуле. Он равен 0,339 и 0,678 соответственно. Эти результаты, как ожидается, будут несколько отличаться от уравнения плоской пластины из-за кривизны поверхности. Однако Для выбранных цилиндров (диаметром 19 и 25,4 мм) радиус кривизны очень велик по сравнению с толщиной пограничного слоя, поэтому полученные свойства являются Плоская пластина. Количество Шмидта на основе воздушного нафталина составило 2,40. В системах с пограничными слоями, где происходит одновременный тепломассообмен и Pr = 8c = 1.0, безразмерный температурный профиль также показан на диаграмме кривая.
Связанный с коэффициентом массопереноса, он может быть расширен до коэффициента теплопередачи. Коэффициент теплопередачи от потока горячего газа, протекающего по плоской пластине、 Она уменьшается за счет массопереноса от поверхности пластины к пограничному слою.1 способ доказать это-ввести 2-й газ через пористую плоскость Пластина на границе layer. At высокие расходы потока, сублимация самой плиты могут произойти, так же, как абсорбция скрытой жары сублимации、 Уменьшение коэффициента теплопередачи в результате эффекта массопереноса только что учтено. Этот эффект может быть достигнут.
Легко испаряется Тарелка. Жидкость с поверхности ?/ —ИИ — — — — — — Я В U’g inu1 Зудящий На противоположный эффект увеличения коэффициента теплопередачи указывает высокий коэффициент массопереноса, который наблюдается при охлаждении пара до насыщенной температуры вблизи поверхности.
Смотрите также:

