Оглавление:



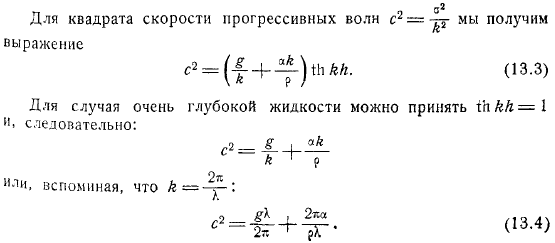



Капиллярные волны
Для скорости распространения прогрессивной длины волны, возникающей под действием силы тяжести, с учетом глубины жидкости. Однако в случае гидромеханики очень коротких длин волн необходимо учитывать влияние так называемой капиллярной силы, поэтому мы видим, что эта формула неверна. Последний возникает в результате взаимодействия молекул жидкости друг с другом и важен только в очень тонком поверхностном слое жидкости.
Рассмотрим элементы поверхности жидкости, которые окружены криволинейными линиями. Действие на поверхности раздела двух жидкостей капиллярной силы на этот элемент происходит так, как будто элемент поверхностного натяжения приложен к каждому элементу по длине кривой и перпендикулярен поверхности жидкости и является касательной плоскостью. Величина a называется поверхностным натяжением.
- Зависит от типа жидкости и от температуры всего (или от типа соседних жидкостей, так как обычно необходимо учитывать контакт воды с воздухом, например).
- Для температуры воды и воздуха. Рассмотрим влияние капиллярности на гравитационные волны.
Ограничивают в случае невращающихся волн плоскость и выравнивают глубину жидкости. Людмила Фирмаль
Потенциал скорости должен удовлетворять уравнению. Давление определяется по формуле внутри жидкости.
Для того чтобы найти условия, которым должна соответствовать свободная поверхность, рассмотрим элементы поверхности с длиной (ширина этого элемента в направлении оси обычно приравнивается к единице). Давление над поверхностным элементом считается постоянным везде и обозначается давлением под очень тонким слоем, под которым возникают капиллярные силы. Тогда силы, показанные выше, должны быть в.
- Сумма проекций этих сил на вертикальную ось равна нулю. Это даст вам следующее. Предполагая, что волна бесконечно мала, ее можно заменить и, следовательно, записать предыдущее равенство в виде.
- Итак, условие на свободной поверхности описывается в виде (в качестве константы возьмем знак производной).
Мы дифференцируем это выражение и заменяем его на сквозное, например. В конечном итоге вы получите следующие условия. Поэтому мы должны выполнить. Как видно из назначения этой функции выражению, удовлетворяются первые выражения .
Получаем следующую формулу для степени скорости бегущей волны. Людмила Фирмаль
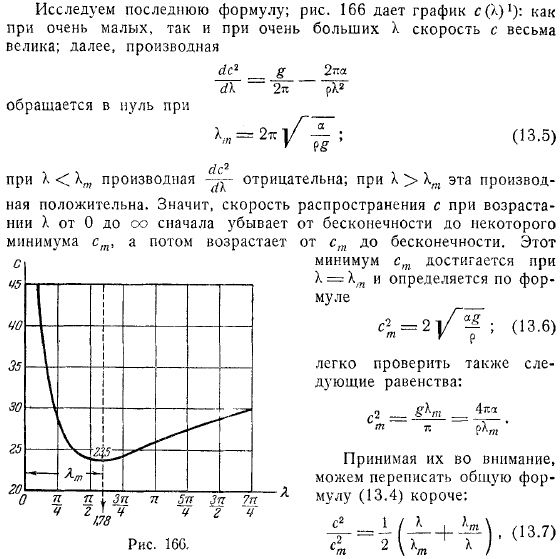
Для очень глубоких жидкостей конечной амплитуды , вы можете принять. Изучите последнее. Отображает графики как очень маленьких, так и очень больших, и скорость очень быстрая.
Дальнейшие производные. Вы также можете легко проверить следующую эквивалентность. Учитывая их, можно легко переписать общую формулу. Если производная отрицательна;когда эта производная положительна. Это означает, что скорость распространения уменьшается сначала от бесконечности до определенного минимума, а затем увеличивается от бесконечности.
Минимальное значение достигается и определяется по формуле. Кроме того, сравнение с показывает, что первый член возникает из гравитации (потому что он не содержит поверхностного натяжения, член возникает из капиллярных сил не включает гравитационное ускорение). Из этой формулы видно, что для крупномасштабных случаев только первый член играет сравнительную роль, поэтому мы можем игнорировать действие капиллярных сил по сравнению с действием силы тяжести.
Если же, наоборот, она мала по сравнению с ним, то первый член играет очень малую роль, и поэтому влияние гравитации ничтожно мало. Более короткая длина волны называется капиллярной волной. Именно поэтому скорость распространения гравитационных волн не может быть меньше определенного минимума.
Следует также отметить, что волны разной длины могут распространяться одновременно. Ясно, что если определенная длина удовлетворяет формуле, то такая же длина удовлетворяет формуле. Кроме того, из этих длин всегда будет длиннее, а другой будет короче.
Потому что так, например, волна распространяется со скоростью, а ее длина удовлетворяет уравнению. Он также показывает цифры для воды и. Этот случай (в системе). Рябь обычно образуется перед телами, которые движутся в жидкости. Если скорость этого движения не медленная .

