Оглавление:















Принцип термодинамического подобия.
- Принцип термодинамического подобия Сравнить свойства различных веществ、 Обычно эти вещества принимают при одной и той же температуре* Давления ту р или круглой при прочих равных значений Параметры.Вопрос в том, есть ли такие Как сравнивать?Не следует сравнивать свойства? Вещества, их проглатывание в другом смысле Состояние, которое»соответствует» друг другу? Открытие критического состояния、
На основе уравнения Ван-дер-Ваальса, полу* Состояние так называемого » приведенного уравнения* 4-е».Уравнение ван-дер-Ваальса записывается в виде: _ РТ ох в 15) Учитывая это, в важный момент、 Отношение а, 14), получаем следующее: ПК -^+?= 0 0.16) К (L2l \ ORT fi / 7 • * Я ^ З^ ————-¦ ¦-Я Я Я 1 / я dV2) т(в-БФ в * в «; Из формул а, 15), а, 16) и А, 17), вы можете видеть: = Ох, Дж. есть _3?。 t_j ох / ю Соотношение а, 18) может быть определено из Важные параметры вещества РК, ВК и ГК являются постоянными.
Принятие законов в каждом штате основан на принципе термодинамического подобия. Людмила Фирмаль
Дейр-Уарзазат и наоборот. Пользуясь тем, что каждое вещество имеет довольно Специфические ключевые параметры ГК, ВКТ РХ могут Введение новых переменных: ^-= я; — ^ = м>; ^ = т,а, 19) Где i, f, t-давление, объем, перепад температуры. Двадцать семь Используя приведенные выше параметры, вы можете написать Уравнение состояния ван-дер-Ваальса Вводятся константы a и b.То есть исключаются отдельные лица Индивидуальные характеристики вещества. 19).: ТК = ^; ВК = ^; а =?。 А, 20) Если подставить эти соотношения в формулу А, 18)、 Мы получаем: Наконец, уравнение A, 21) подставляется в уравнение Ван дер Ваальс получает следующий вид уравнения: 1)= 8Т. а, 22) Это уравнение называется приведенным уравнением.
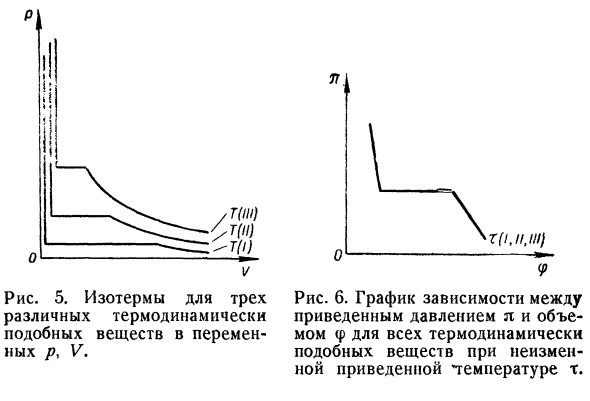
Государство.Потому что он содержит только указанные Это количество, а не количество, которое указывает на определенную характеристику Различие между веществами и другими веществами.Равный Уравнение а, 22) является уравнением всех состояний Ван дер Зваан Валенсой. По наличию формулы а, 22)、 Понятие соответствующего государства; 2 государства или не государства Некоторые вещества, которые являются одинаковыми Введенные параметры i, q> и m называются соответственно Сопутствующие условия. Законы каждого государства формулируются следующим образом: Если 2 или более вещества являются удовлетворительными То же самое приведенное уравнение состояния Из приведенных 3 параметров имеют одинаковые 2 л, ср, т,в этом случае, они Есть такой же 3-й параметр. Критическое состояние вещества (i = 1, φ= 1、 m = 1) — состояние каждого из них.Взятое количество Вещества в этом случае не играют никакой роли. При наличии соответствующего государственного закона、 Введение нового понятия, имеющего большое значение для термодинамики- Термодинамического подобия, аналогии термодинамического Вещества, подпадающие под действие аналогичных законов Двадцать восемь Рисунок 5. 3 изотерма Термодинамически различных Изменение аналогичных веществ Переменные p, V \ Д А, 11.1 / 1) П Рисунок 6.График взаимосвязей между Декомпрессия p и объем Термодинамически весь объем f Постоянные аналоговые вещества Постоянная пониженная температура т. 1 же удовлетворение, как работоспособного состояния То же уравнение состояния, что и дано.
- Важность термодинамического подобия Что это дает представление о 1 характеристике Если известны другие свойства, то необходимо использовать материал.Например, координаты l, (p, t, термодинамика В таких веществах получается 1 кривая.Рассчитывать Графики параметров P, V, T имеют вид、 Каждое вещество(рисунки 5 и 6).Поэтому, чтобы знать Например, давление 1 вещества Р Значение декомпрессии для нахождения любого давления Р Другие термодинамически подобные вещества、 Если вы знаете его имя. Кроме того, например, если вы знаете графические зависимости、 Температурная зависимость изотермических коэффициентов Сжимаемость одного вещества легко вычислить Расчет других коэффициентов теплового расширения Термодинамически подобные вещества, применение Соотношение Пи П2 ПЗ / 1 С) О РК РК РК РК Если вы знаете хотя бы 1 р-значение процента- Вещества, представляющие интерес. 29 декабря Не все вещества соответствуют закону.
Сопутствующие условия.По существу, он используется для Отдельные группы substances.So, соответствующие законы Состояние некоторых групп достаточно удовлетворительное Органические вещества, такие как отдельные углеводы Углеводороды и связанные с ними заливы Вещество.Однако, во многих технических приложениях Принцип термодинамического подобия этих отклонений Вы можете игнорировать его. D задачи и упражнения 1. / = = 20°C и/?Для азота= 0.134 атм а = 0,00368 и/ (=0,00368.Рассчитайте степень сжатия. Повторите B = 2.
Решение представляет коэффициент изолятора Изотермическая сжимаемость любой жидкости с пониженными параметрами, и и т В связи с Т Где/> K, VK, Gk-критическое давление, объем, температура Температура Отсюда ’Альфа’ Людмила Фирмаль
Коэффициент объема показан на рисунке Идеальное расширение а и степень сжатия РГ Равный газ: Найти числа этих коэффициентов на 1 град И 1 mmHg.Art.In нормальное состояние: G = 273°K、 / 7 = 760 мм рт.Искусство. Повторить = 0.00368; (Ср = 0.00132 3.Найти коэффициент объемной гонки* Разложение A и сжатие pt уравнения ван-дер-Ваальса И много ремней. Повторите а) для уравнения ван-дер-Ваальса: ля¦ == У2)РТВ б)случай уравнения Бертелло: В \ * В-б) 4.Использование уравнения ван-дер-Ваальса ca определяет изотермическую скорость звука.
По определению индикации, изолятор- Изотермическая скорость* \ Ф 1Т Где m-масса молекулы массой 1 грамм. 5.Использование формулы для расчета A, 18) постоянная ван-дер-Ваальса A, b и отношение Используйте следующие важные параметры (、 Вещество: Метилацетат Метилформиат 506.9 487.2 РК (атм)) 46.33 59.25 227.6 172.0 Повторный метилацетат: Л2 * атм а = 10,6- mol2 все Метилформиат: 6.Создать критический для критической связи Параметры и константы уравнения состояния Берта- Для A, 11) используйте формулу A, 14). 7.Установите аналогичным образом Связь между важными параметрами и константами Уравнение Клаузиуса A, 10). 8.In аналогичный способ установления Связь между важными параметрами и константами Уравнение детеричи: Показания первый и 2-й про- производная от P, то производная в P, также исчезает Она исчезает.
Повторите ПК〜 9.Пожалуйста, проверьте выше Уравнение состояния для параметров i, f, t Камерлинг-Оннес Данная форма: 10.Для вещества показано, что оно рассчитывается* Будьте справедливы и уважайте законы каждого государства- Живое отношение | ^ = — ^ , А, 24) fV2 Пх Где rg и rg-коэффициенты изотермического сжатия 2. скорость уплотнения одного вещества; pKi и p-критические давления, соответственно. 、 Для другой жидкости критического давления ИПК Коэффициенты изотермического сжатия имеют аналог Схожие взгляды: 1(дц2 \ 2 f2Rk2 [dl2) предполагая φ1=φ2 (это、 Количество жидкости хорошо контролируется законом Соответствующее состояние), то получим отношение A, 24、 То есть коэффициент rg соответствующего состояния Он пропорционален критическому давлению этих жидкостей Жидкость.
11.Для зависимых от психоактивных веществ、 Соблюдать законы каждого государства Соотношение: Где ax и a2-коэффициенты объемного расширения Вещество GK2 и TK1 имеют критическую температуру, соответственно Температура. Решение.Идти по следу При решении предыдущей задачи мы представляем коэффициенты Объемное расширение вещества a = ’ yy [- dm〜) Указанные параметры являются я, ср. и Т. В свою очередь, уравнение а для первого вещества имеет вид Смотреть: 3 В Ф Ноздрев 33 Для 2-го материала при критической температуре ГКГ Коэффициент расширения Тома записан в аналоге Точно так же: Оба вещества Для соответствующего состояния, то их П\ = 22 \ Два
Смотрите также:
Решение задач по термодинамике
| Уравнение состояния для Камерлинга Оннеса. | Первое начало термодинамики. |
| Критическое состояние вещества. | Понятие элементарной работы. |

