Сила действия струи на стенку

Сила действия струи на стенку

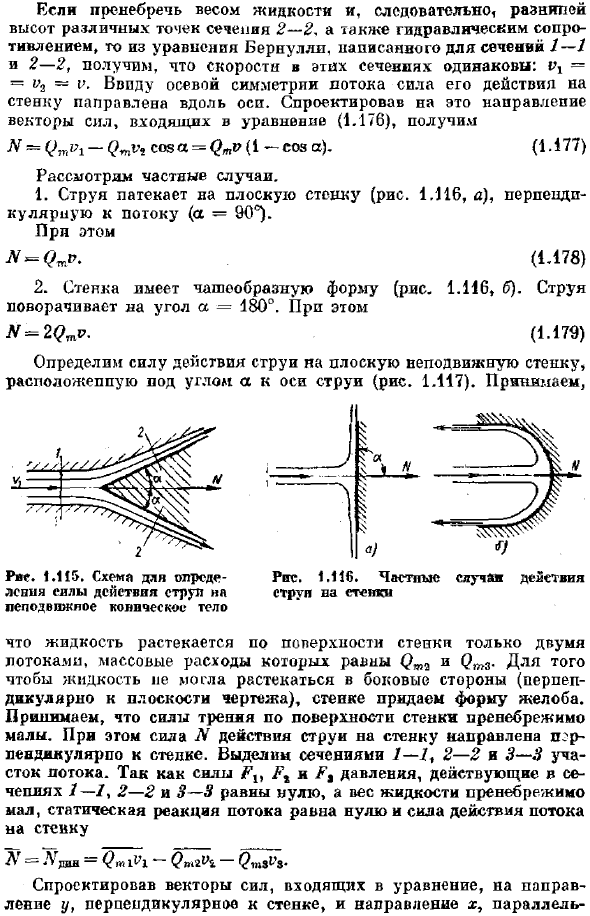
Сила действия струи на стенку. Определите силу действия свободного потока, вытекающего из отверстия или сопла неподвижного стейка. Сначала рассмотрим коническую стенку с осью, совпадающей с осью струи (рис. 1.115).Для секций 1-1 и 2-2 выберите секцию потока. Секция 2-2 представляет собой плоскость вращения. Давление на входе 1-1 и выходе 2-2 секций равно атмосферному давлению, поэтому сила Р%и давление пули равны. Вес выбранного сечения потока равен ignored.

Эта задача является частным случаем задачи определения силы воздействия потока на стенку канала, которая рассматривалась в предыдущем пункте. Людмила Фирмаль

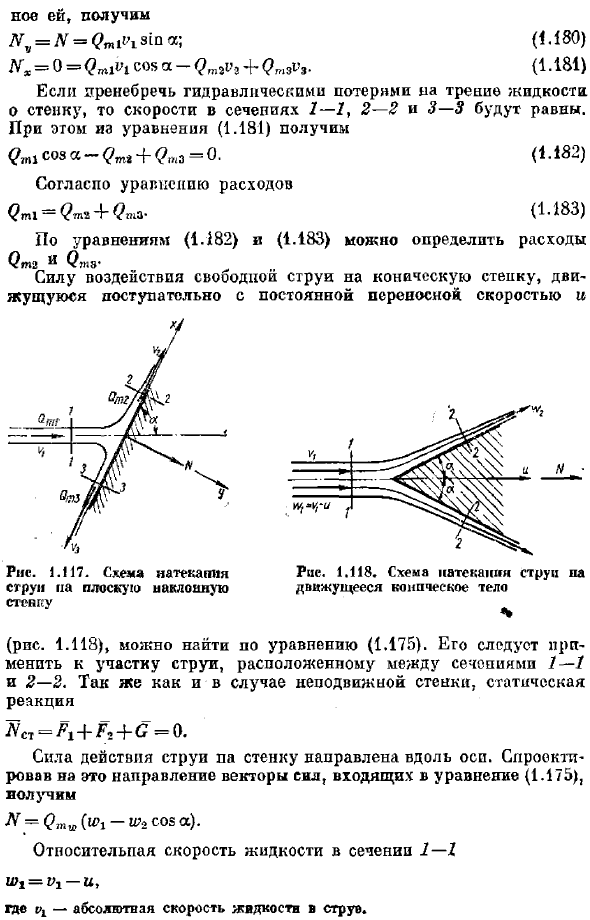
• In в этом случае реакция статического потока LH = ^ 1 + ** + C = 0 и IN-fs.^ 1-(1.176） I: мы игнорируем вес жидкости и, следовательно, различные высоты * raenipey секции 2-2 точек, а также гидравлическое сопротивление типа Бернулли, написанное для секций 1-1 и 2-2, мы находим, что в ehah скорость равна частям! = V2-V. Благодаря осевой симметрии потока сила, действующая на стенку, направлена вдоль оси. Если спроецировать вектор сил, входящих в уравнение (1.176) в этом направлении, то получится: Н = соѕ а =(1-С05 а), (1.177） Рассмотрим особые случаи. 1.Струя течет к плоской стенке, перпендикулярной потоку (рис. 1116, а) (а-90°). В то же время Л.= (4L78） 2.

Стена имеет чашеобразную форму(рис. 1.146 * б).Струя вращается под углом α1= 180°. в атоме Н ^ 2(2 ^(1.179） Определить рабочую силу струи на плоской неподвижной стенке, расположенной под углом α к оси струи(Рис. 1. 117).Принимать Жидкость растекается по стенке всего 2 потоками, ее массовый расход равен 02t3.To предотвратите растекание жидкости в стороны (перпендикулярно плоскости рисунка), придайте стенке форму паза. Предположим, что сила трения на поверхности стены равна negligible. In в этом случае сила N реактивного воздействия на стейк направлена перпендикулярно шагу. Раздел 1-7 * 2-2 и 3-Выберите в разделе потока.

• Давление p% и Es, действующие на секции 1-7, 2-2 и 3-3, равны нулю, а вес жидкости пренебрежимо мал, так что статическая реакция потока равна нулю, а сила потока, действующая на стенку, равна нулю. ГД•1 Л ^ ДДН-1 ^ 1 ~~ Рассчитайте вектор силы в уравнении в направлении Y, перпендикулярном стене, и направлении x, параллельном стене: НГ = Н = ^ м ^ в ^ с ^ АА■, (1.180） АР * −0 = 0Zt1!。 ! Co » и 0?gag1> g + 0?ga31> ы. (1.181） Далее по формуле (1.181) ^ 1П, co8a ^ В4 +(?М3 = 0.(1.182)） Согласно уравнению расходов $ Т \-4 ″ ЗСТ (1.183)） Из уравнений (1.182) и (1.183) можно определить стоимость ^ Т2 ^ ^ В8 ′ Действующая сила свободной струи на стенку конуса поступательного движения при постоянной скорости переноса (Рис.1.118) можно найти в Формуле (1.175).

Если не учитывать гидравлические потери из-за трения жидкости о стенку, то скорости секций будут равны. Людмила Фирмаль

• Она должна применяться к секциям струи, которые находятся между секциями 1-1 и 2-2.Статическая реакция, подобная неподвижной стене NC1—\ Я2″} » €r-0. Сила воздействия струи на стенку направлена вдоль оси. Так как мы проектировали вектор сил, входящих в уравнение (1.175) в этом направлении、 И-0?Г(Л> 1 ^ 2 С05 а). Секция 1-1 относительная скорость жидкости tg-Vx-и Где u1-абсолютная скорость жидкости в струе. Из уравнения относительного движения Бернулли игнорируют разницу между гидравлическими потерями и высотой точки в разделе 1-1-n2-2. Стена (2мн = П(^ 1 -«)* 5 \ Где 8-площадь струи. Следовательно, сила действия струи на стенку П = Р5 (В1-у)*(\АУ).

Смотрите также:

Методические указания по гидравлике

Возможно эти страницы вам будут полезны:

1. Гидравлический удар.
2. Силы действия потока на стенки канала.
3. Уравнение моментов количества движения для установившегося движения жидкости в равномерно вращающихся каналах.
4. Основы теории лопастных насосов.