Профиль волны

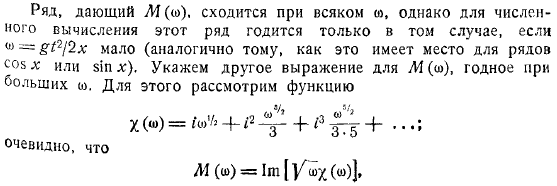
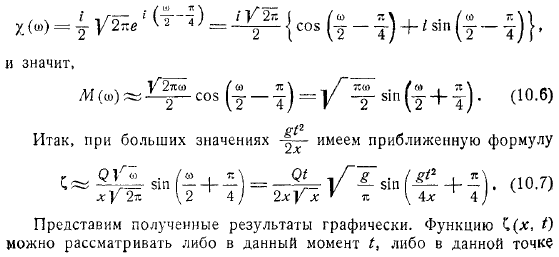
Профиль волны

Приступим к изучению результирующего волнового движения. Мы ограничиваемся только рассмотрением профиля волны и происходящих в ней изменений. Как известно гидромеханика, и профиль волны определяется из уравнения.

Таким образом, что получается из уравнения. Поэтому, когда мы вводим обозначения. Это выглядит так. Функция в скобках. Любой ряд, который сходится, но для численных расчетов этот ряд подходит только в том случае, если у плоской задачи он мал (аналогично тому, как это делается в серии).

• Указывает другое представление, которое подходит для больших. To сделайте это, рассмотрим функцию. Где знак обозначает мнимую часть комплекса.
• Если мы интегрируем это линейное дифференциальное уравнение, мы видим, что.

Но, следовательно, это означает. Людмила Фирмаль

Для простоты можно рассмотреть только случай очень большого, а при нахождении приближенной формулы заменить верхний предел интеграла. Но потом, после замены, это выглядит так.

Мы использовали так называемый интеграл Френеля. Поэтому для больших значений существует приближенное выражение отображает результаты графически. Функции могут рассматриваться в данный момент или в определенный момент времени Ось.

• Представляет представление функции на определенный момент времени. С тех пор тогда для больших: следовательно, малый масштаб должен быть рассчитан по.
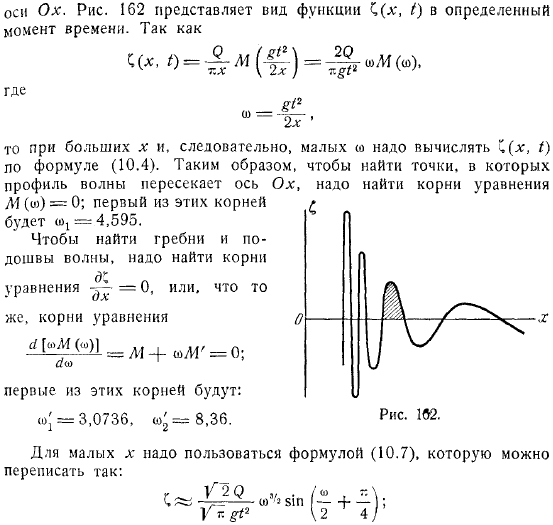
• Чтобы найти точку, в которой профиль волны пересекает ось, нужно найти корень из.

Будет первым из них. To найдите гребень и дно волны, вам нужно найти корни уравнение или. Что-то. Корни уравнения Это будет первый из таких маршрутов. Для небольших случаев следует использовать выражение, которое переписывается следующим образом.

Это показывает, что многие волны могут быть получены, если они малы и, следовательно, велики. Людмила Фирмаль

Волна короче, выше, и чем ближе точка задачи к началу координат, тем она выше. Сам случай, точка пересечения оси и профиля определяется из условий.

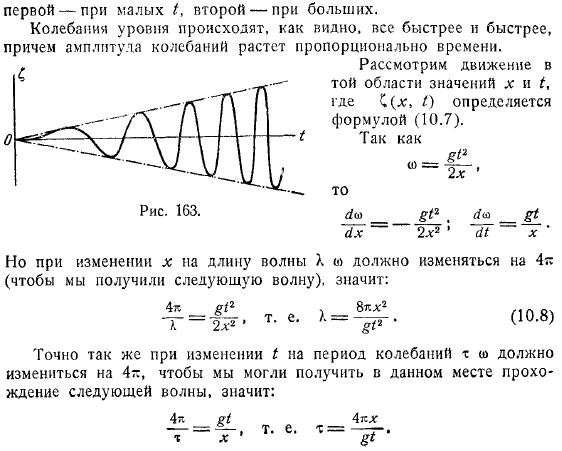
Расстояние между соседними точками равно по мере ее увеличения она уменьшается. Амплитуда волны увеличивается пропорционально на градуса. Формула выглядит следующим образом.

Поэтому по мере его увеличения удельное значение перемещается с ускорением. Чем она меньше, тем больше значит сама по себе. Увеличивающийся профиль волны расширяется пропорционально мощности времени, и вертикальная ордината также уменьшается таким же образом (при этом область, окруженная любой волной, не изменяется).

Теперь рассмотрим, чтобы быть представителем в этом. В этом случае при конечной глубине жидкости используйте выражение. Первый маленький, второй большой. Как видим, колебания уровня происходят постепенно быстрее, а амплитуда колебаний увеличивается пропорционально времени.

Рассмотрим движение в определенном диапазоне значений. Однако, если длина волны изменяется, она должна быть изменена так, чтобы можно было получить следующую волну. Аналогично, когда изменяется в течение периода колебаний, необходимо изменить так, чтобы он мог получить прохождение следующей волны в указанном месте.

Наконец, чтобы определить полную скорость распространения, нужно отслеживать движение гребней. Но так как горе всегда соответствует одна и та же величина, то она изменяется по формуле, скорость волны равна. Тогда получим известное выражение из этого мы можем видеть, что групповая скорость явно равна из уравнения, потому что групповая скорость представляет собой скорость, с которой распространяется волна определенной длины.

Здесь становится понятно, почему рассматриваемая волна движется с постоянным ускорением. Поскольку волны, которые движутся больше вдоль оси, длиннее, они движутся с большей скоростью, и поскольку многие волны постоянно растягиваются, скорость движения этих волн увеличивается все больше и больше, и они движутся с постоянным ускорением. Конец вершины первой волны равен, дна волны.

Таким образом, вы получаете следующую диаграмму: начало координат излучает бесконечную последовательность волн в обоих. Дело, конечно, в рассмотренном нами случае, то есть невозможно осуществить начальное восхождение конечной массы жидкости на бесконечно малую часть оси.

Если ту же жидкость поднять в область оси длины, то причины некоторых из них перестанут быть истинными. То есть вывод справедлив только в том случае, если длина рассматриваемой волны больше в сравнении. Отношение Кроме того, отношение должно быть большим по сравнению с единицей, так что результат может быть применен.