Оглавление:





Свойства парциального мольного объёма. Смысл производной
Характер частичного мозаичного объема значение дифференциации (dV] dni) r, v Производная V {- ( — — — ) является пределом отношения at-V dm / m, p (в drii 0). Увеличение объема dV относительно числа молей drii добавляется в систему при постоянных T и py, вызывая это изменение объема.
Это значение также равно увеличению объема при добавлении в раствор 1 моля компонента i, и ясно, что его начальный объем очень велик по сравнению с молярным объемом компонента L. Поэтому скажите мне количество воды и определенное количество этилового спирта, равное молярной смеси.
Добавьте 18 см5 воды в эту смесь. то прирост объема составляет не 18, а всего 16,5 см3. Этот размер является частичным молярным объемом воды в данном растворе.
Если первоначальный объем был достаточно большим Людмила Фирмаль
И получается, что сумма V равна negative. So например, если в водный раствор этой соли добавить магний-спиртовую серную кислоту, то объем раствора уменьшится.
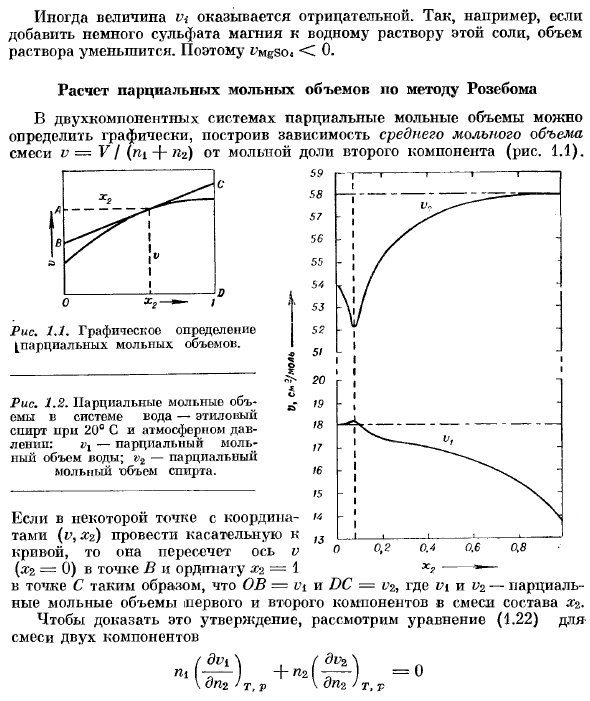
Таким Образом, I > Mgso < < 0. Расчет частичного молярного объема с использованием метода Rosebom В двухкомпонентной системе парциальный молярный объем может быть определен графически путем построения зависимости 2-го компонента среднего молярного объема v = VI (rii-f n2) смеси от молярной доли (рис.1.1). Рисунок 1J [графическое определение частичного молярного объема.
Рисунок 1.2.Парциальный молярный объем воды-20 ° С и система этилового спирта при атмосферном давлении: vx-парциальный молярный объем воды; v2-парциальный молярный объем спирта. В определенных точках координат (vzz) нарисуйте касательную к 13 Кривая, она пересекает ось v 0 h * w (#2 = 0) точка B и ордината x-2 = 1 x? ——— OB = vi и DC = 1%так, что в точке C, vi и v2 находится частичный молярный объем 1-го и 2-го компонентов в смеси состава Xz.
Для доказательства этого утверждения рассмотрим уравнение смеси 2-х компонентов (1.22). ЛП(ДПГ Р ПГ (ДПГ) Т
Или после деления на L、 О + * ( * «)=. (1.33) Дп2 в ’т, р дп2 в’ т, п Как показано, молярная фракция может быть использована для представления частичного молярного объема с интенсивными переменными. Итак, если вы выберете # 2 в качестве независимой переменной, вы можете написать: = Вт (ТТП, Х2) = Ви [T9pt-Р—). \ / г » + с ИРТ-Ф Р2. Таким образом, легко показать, что (1.33) переписывается в следующем формате: Н(*!) + ХС [^ П = 0. (1.34) В dx2 ′ т, р dx2 в; т, п
Кроме того, если V = pm — {- «r’ — ’ r делится на (ni + / r2)、 в = Х ^ ви + Z2V2 =(1-Х2) Ви-Ф x2v2(1.35) после дифференцирования на n, z?2 ноября. + * +(1-^(£1。, + Х2 (Си.、• Согласно (1.34), последние 2 условия сокращаются、 (dx2) т, п Повесьте Xr с обеих сторон, и вы можете видеть (dv \ x2-r — = — x2vt =(ZD2 + XiVt) — (XiVi + x2Vi) \ Почтовый индекс ox2 не. В Или Г = в-Х2 (- П^ -) = 0 А-Б а = Обь \ 0Х2> Т, П Кроме того, вы можете указать=•постоянного тока. Возвращаясь к примеру смеси воды и этилового спирта, частичный молярный объем воды Vi и спирта ig показан на рисунке 1.
Обратите внимание, что 1.2 обнаруживается для обеих кривых с одинаковым значением x ^, в зависимости от x2.It основано на Формуле (1.34), когда пуля работает, нечетное число кривой равно нулю, а градиент другой кривой должен быть равен 1. (1.34).Например, предположим, что x2 стремится к нулю.
Максимальный молярный парциальный объем Поведение парциальных молярных величин в экстремальных разведениях можно исследовать с помощью урабупина Людмила Фирмаль
Здесь могут возникнуть 2 случая.(dvi 16×2) m, v стремится к нулю или может оставаться в конечном amount. In в последнем случае дифференциал (dig! Dxr) r, p будет бесконечным. Это связано с тем, что произведение отношения x2 / xt на пулю остается конечным. Обе эти возможности схематично показаны на схеме. 1.3 и 1.4. (1.36) = В-В.
Экспериментально было обнаружено, что реальная система характеризуется поведением, соответствующим фигуре. 1.3 2. в x2-0 производные (dv \ I dxr) r, p также стремятся к пуле, и частичный молярный объем компонента 1 приближается к Молярному объему 1 в чистом состоянии быстрее, чем линейная зависимость vt от x2. 。
Смотрите также:
Решение задач по термодинамике
| Давление пара и свободный объем | Энтропия плавления |
| Энтропия плавления | Многофазные системы. |

