
Тип работы: Задача
Предмет: Сопротивление материалов
Статус: Выполнен
Год работы: 2020
Страниц: 1
Оригинальность: 97% (antiplagiat.ru)
Формат: Скан (Рукопись)
Цена: 291 руб.
Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
Благодаря этой странице вы научитесь сами решать такие задачи:
Помощь по сопромату и решение задач на заказ
Другие похожие задачи:
| Задача 3.7. Для сечений с одной осью симметрии | Задача 4.2. Стальной круглый вал сплошного сечения |
| Задача 3.8 Для обратно симметричных сечений | Задача 4.3 Стальной полый стержень сечением |
Описание работы:
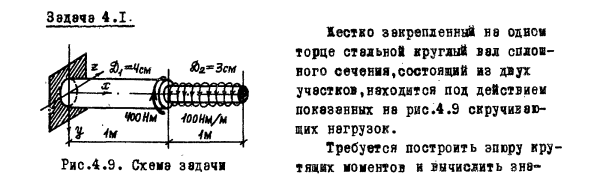
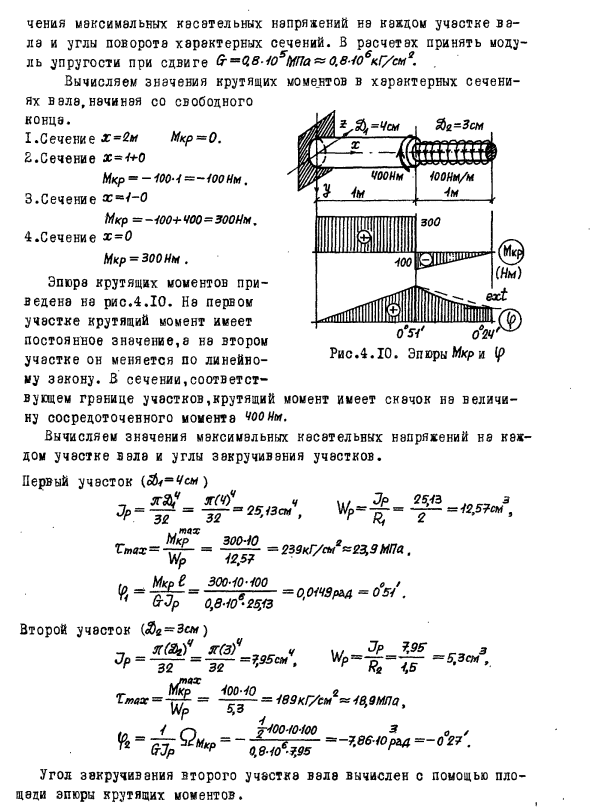
Задача 4.1. Жестко закрепленный на одном торце стальной круглый вал сплошного сеченая,состояний из двух участков,находится под действием показанных на рис.4.9 скручивающих нагрузок. Требуется построить эпюру крутящих моментов и вычислить значения максимальных касательных напряжений на каждом участке вала и углы поворота характерных сечений. В расчетах принять модуль упругости при сдвиге. Вычисляем значения крутящих моментов в характерных сечениях веле начиная со свободного конца. 1.Сечение Эпюра крутящих моментов приведена на рис.4.10. На первом участке крутящий момент имеет постоянное значение,а на втором участке он меняется по линейному закону. В сечении,соответствующем границе участков,крутящий момент имеет скачок на величину сосредоточенного момента 400 . Вычисляем значения максимальных касательных напряжений на каждом участке вала и углы закручивания участков. Первый участок. Угол закручивания второго участка вела вычислен с помощью площади эпюры крутящих моментов.Определяем угол поворота торцевого сечения вала. Торцевое сечение поворачивается по часовой стрелке. Эпюре углов закручивания вала показана на рис.4.10. На первом участке углы закручивания меняются по линейному закону,а на втором — по закону квадратной параболы.
Определите силы в ножках вышеприведенной таблицы, когда нагрузка применяется в точке с координатами у Подсказка.
