Оглавление:









Теплообмен при развитом профиле скорости в трубе
- В наиболее распространенных задачах теплообмена необходимо учитывать нагрев и охлаждение жидкости в трубе. Рассмотренный входной эффект может существенно повлиять на общую работу коротких элементов оборудования.»Самое интересное, если входной эффект незначителен. Профиль скорости развитого изотермического ламинарного течения имеет форму параболы.Формула этого профиля была впервые выведена в этой книге.7 из уравнения баланса Импульс, второй последовал. 12.
Из уравнения движения и уравнения непрерывности.Их формат-thems = 2b [1 — (^Y].<24.15) при нагревании или охлаждении жидкости. Из-за влияния температуры на вязкость профиль скорости может сильно варьироваться.Поскольку сложность результирующей задачи теплопередачи очень велика, приблизительно Решение. 1 re [55] показал решение для 2 случаев. 1 заключается в том, что искажение профиля считается малым, а параболический профиль является retained.In другое решение, это искажение Строго указано, что распределение скоростей по поперечному сечению считается равномерным.
Как следует из определения, тепловой поток (1-ц Если теплопроводность не зависит от температуры, то, как видно из рис.12. Людмила Фирмаль
Поток Ханоя называется штоковым или поршневым потоком. Это предположение можно почти выполнить, если: Жидкость нагревается от стенок трубы(рис. 23. 1). Решение Гретца считается Тараболическим профилем скорости.Решение состоит в том, что осевая составляющая скорости Любая точка трубы вычисляется по формуле (24. 10) определяется граничным условием, предполагается, что температура стенки везде одинакова, а входная температура жидкости постоянна Дифференциальное уравнение энергии 10.
Может быть описан в цилиндрических координатах, а в случае осесимметричного стационарного состояния: e (если Уравнение (24.16) предполагает, что теплопроводность направления потока считается пренебрежимо малой по сравнению с режимом переноса DRS. Формула (24. 15) в уравнении энергии вы получаете d2g. 1st _ 2 » b dg2’g dg / dh, 1. d2 * \ \ dg2r dg ‘ dx2)*(24.16)
Решение уравнений с участием I и x выражается в виде экспоненциальной функции.Решение Уравнения, связывающие I и g, представлены рядом.Сочетание этих решений дает формулу.(24.18) значения констант Bp и pn являются для первых 10 членов ряда, подвалов, притоков и Клейн[147].в той же работе есть выражение для определения функции, то есть.
Для определения средней температуры или температуры смешивания кратко рассмотрим пример 4.2. Вы можете найти местный коэффициент теплопередачи ah. Напишите уравнение теплового баланса в основном сечении трубы xx: «x (lR xx) (I. — 1b)=] USR y1b. уравнение выглядит так: Xp Lx 18-1(24.20) Формула для локального коэффициента теплопередачи AX после умножения обеих частей на Г-это формула для числа местных нуссельта-г -.Таким образом, преобразование формулы (24. 18).
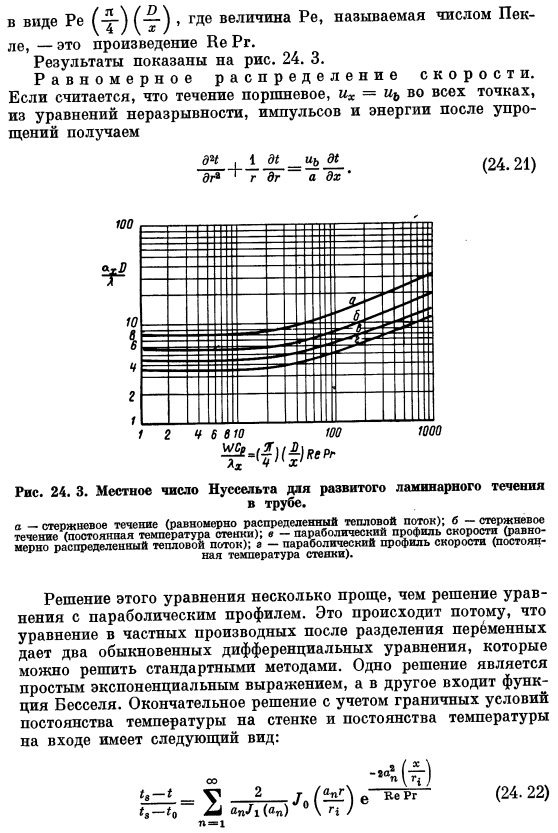
Наконец, получено сложное уравнение, описывающее параметр Kih как функцию выражения, известного как граф ГРЕТСА. Это выражение можно расширить. Сумма Pe, которая описывается в виде Pe ( — ) и называется числом пекле, является произведением Ke Pr.Результат показан на рисунке. 24. 3.Равномерное распределение скорости.Если в это верят После упрощения из уравнения неразрывности, импульса, энергии, течения поршня во всех точках,=и*(24.21) 24.
Локальное число нуссельта развитого ламинарного течения Ток в трубе. а-поток сердечника (равномерно распределенный тепловой поток); б » стержень^трехмерный (постоянная температура стенки); в — параболический профиль скорости (Равномерно распределенный тепловой поток); а-параболический профиль скорости (постоянная температура стенки).Решение этого уравнения несколько проще, чем решение уравнения. Профиль параболы.Это связано с тем, что после разделения переменных дифференциальное уравнение в частных производных дает 2 обыкновенных дифференциальных уравнения, которые могут быть решены. Общепринятые методы.
Решение-это простая экспоненциальная формула, а другое решение-функция Бесселя.Окончательное решение с учетом граничных условий гомеостаза Температура стенки и постоянство температуры на входе принимают следующий вид:^ 8 * = * 8〜* 0 2 n = 1 2 g (^\»nLOp)° / e Be Pr(24. 22) величина an является корнем N-уравнения (ap)- O, Yo и A-функции Бесселя нулевого и 1-го порядка в стандартной таблице.Детали решения приведены в статье, приведенной ранее с учетом проблемы О потоке с параболическим профилем скорости.Средняя температура(24. 19) уравнения упрощаются при применении к утечкам сердечника, потому что они= u. из-за этого (24.23) Max 1b, формула.
Можно использовать для нахождения локального коэффициента теплопередачи ah.Затем мы используем этот коэффициент для вычисления локального числа нуссельта-u. это выражение Формат важной величины: n = 1 X 2ap-e KeRg P-1 (24. 24) эта зависимость показана на рисунке. 24. 3.Равномерный тепловой поток.Об обоих принятых на предыдущей странице В схеме течения получены другие решения, когда граничные условия постоянной температуры ступеней заменяются условиями равномерного удельного теплового потока через стенки.Локальное поведение Число нуссельта в этом граничном условии показано на рисунке. 24. 3.Для всех случаев, показанных на рисунке. 24.
Местный номер нуссельта длинный, крупный план, как вы можете видеть Труба, которая ограничивает значение.Для однородного теплового потока эти пределы могут быть рассчитаны без полного решения исходного уравнения, как показано в Примере 24.2.Пример 24. 2. в случае равномерного теплового потока в жидкость локальное число нуссельта в стержневом потоке в длинной трубе стремится к 8.Непрерывности, движения、 Энергия в этом случае зависит от формулы (24. 21) получает: dH, 1 d1 cP.Если тепло подается с одинаковой интенсивностью на единицу длины трубы, то температурный профиль Расстояние от входа до трубы имеет тенденцию быть определенным shape.In эта область-всегда во всех отношениях формула(24.
Может быть записан в формате E2 ) * температура на заданном расстоянии от оси может быть представлена s Интегрируем уравнение(1).Это делается в стандарте way.As новую неизвестную переменную возьмем-и уравнение(1) станет уравнением 1-го порядка.
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Расчёт найти определения | Учебник |
- Интегрировать непосредственно. После интегрирования уравнение температуры становится 1n r — {‘C 2 — (3) формой для определения любых констант C \и C2 по граничным условиям. для r = 0-= 0, для r =-1 = использовать dg P. решением является функция(6). в уравнении(6) r является функцией x, поэтому она<= f(r, x).Если вы хотите интегрировать эту формулу в соответствии с Формула 24.
С помощью которой средняя температура будет равна (7) (8) получим отсюда формулу разности температур и подставим ее в Формулу (4) и axP _ cP2 32 X-4сО «» 8、 Средние шансы.Для расчетов полезно знать средний коэффициент теплопередачи всей трубы.Если температура поверхности равна ha, но это означает среднюю температуру на выходе из трубы、 Среднее арифметическое коэффициента aa области A можно определить по формуле: g = aaA * ■ > A = a » 4 (;,_<>) a. (24.25) в этом уравнении d =] USR (1L1-M, A = лм соотносят эти выражения 24.
Количество тепла, проходящее через единицу площади поверхности за единицу времени, называется тепловым потоком. Людмила Фирмаль
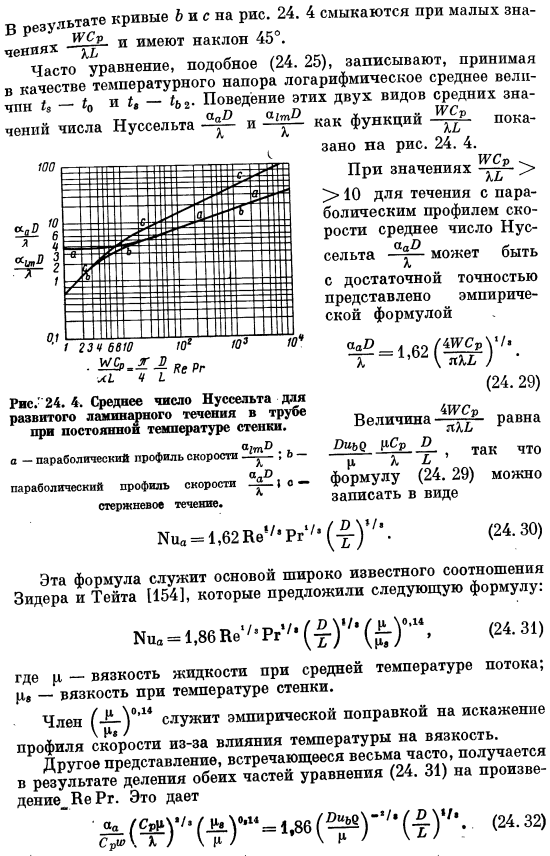
С длинной трубой При низких скоростях потока средняя температура на выходе 2 приблизительно равна температуре стенки/ а, поэтому уравнение (24. 26) упрощается: OdR _ 2UUSr X YaKhD *эта упрощенная формула является、 Течь с закрученными и параболическими профилями скорости. (24.28), кривая B и C на рис.24. 4 замкнут с небольшим zn-R i’SR и имеет наклон 45°.Часто Уравнение типа ‘ (24.25) записывается и принимает логарифмическое среднее значений I, -10, I, r _ _ _ ^ ttttttohhh-PPPPPPP. ■Nusselt Aab a1tV-u и-рисунок 24. 4.Среднее число нуссельта в развитом ламинарном потоке в трубе при постоянной температуре стенки. а1т ^.
На рисунке показано поведение этих 2 типов средних функций. 24. 4.»\USR > > 10 для потока с параболическим профилем скорости среднее число нуссельта определяется эмпирической формулой(24. 29) могут быть представлены с достаточной точностью. Итак, формула (24.29) равна (24.30) Li = 1.62 Be’/, Pr’ /、(-^-)、/ ‘ее можно записать в следующем формате: эта формула лежит в основе широко известного соотношения сидера и Тейта[154]. Мы предложили следующую формулу: (24. 31) Kia = 1.86 Ke ^Рг’7 * (у -) ‘7 * здесь и находится вязкость жидкости при средней температуре потока.
D-вязкость при температуре стенки.Член совета директоров Эмпирическая коррекция искажения скорости за счет влияния температуры на вязкость. еще один взгляд, который бывает очень часто!»Оба кричат в результате раскола Уравнение произведения Be Be Pr(24. 31) часть этого даст 32.Предел применимости этого уравнения исследованы Макадамс [108]. Данные можно найти в Формуле (24. 32) отклоняется до 250% от указанного значения.1.
Одна из возможных причин заключается в том, что это выражение является Он был разработан, но в короткой трубе входной эффект, описанный ранее, может быть больше.Но, к счастью, предположение о развитых свойствах потока является、 Коэффициент теплопередачи ниже фактического значения, полученного при наличии входного эффекта.Поэтому расчет развитого потока является четким、 Есть дополнительная маржа.Задача 24. 1.Смазка нагревается в теплообменнике «труба в трубе».Масло поступает во внутреннюю стальную трубу с внутренним диаметром 27 при температуре w, 40°C, он выходит наружу со скоростью 0,3 м / с при 33 мм, 70°C.
В кольцевом пространстве между трубами содержится пар, который конденсируется при 104°C. коэффициент Теплопередача конденсированного пара 10 000 ккал / м? H * город.Найдите длину нужного теплообменника.Масло имеет следующие средние физические параметры: плотность 900 кг / м *、 Теплоемкость 0,47 ккал / кг * град, теплопроводность 0,10 ккал / м * ч * град. 24. 2.Исправить проблему теплопередачи на постоянный ламинарный поток Температуру стенки исследовал Левек * [101].Предполагается, что параболический профиль скорости полностью развивается до того, как жидкость войдет в этот участок трубы.
Начнется отопление.Затем температурный пограничный слой развивается и перекрывается с уже сложившимся параболическим профилем скорости.Для локального коэффициента теплоотдачи ах、 Определяя тепловой поток при разнице температур <8-e0, Левек получил следующее уравнение 1Hx = 1.077 (•y) 1 / He/Tg,/. В области Be, Kr> 10, это выражение представляет число нуссельта Такое же значение получено из приведенного на рис.
Комплексного решения Грета развитого параболического профиля скорости, поскольку уравнение Левека не подходит для точки Здесь температурный пограничный слой достигает оси трубы, а область, где он совпадает с общим решением ГРЭС, является измерением длины распространения температурного пограничного слоя или Влияние входного сигнала температуры.Добавьте эту длину к диаметру трубы числа Рейнольдса 100, 1000, 2000 и используйте воздух, воду, светлое масло и ртуть на 93 ° C. жидкость Rg Воздух…………… -Я не уверен. 。 。 0,72 воды……………………… 1.88 светлых нефтепродуктов………….. …… 62 Меркурий……………………. 0.016 24. 3.Соотношение(24.
Не применяется Жидкость с числом Прандтля менее 0,6.Определить коэффициент теплопередачи при критическом числе Рейнольдса Вех = 500 000 при движении ртути вдоль плоской горизонтальной пластины Температура 93°C.At эта температура, число Прандтля ртути составляет 0,016. 24. 4.Дифференциальное уравнение в частных производных распределения температуры нагреваемой жидкости Ламинарное движение с параболическим профилем скорости является формулой для первой половины этой главы (24. 17).Отображение таким же образом, как и в примере 24. Для очень длинных труб с равномерно распределенным тепловым потоком локальный предел числа нуссельта равен 48/11. 24.
Жидкость c равномерным распределением на входе Температура / постоянная масса перемещается слоями со скоростью Вт кг / ч * м2 в замкнутом канале прямоугольного сечения, поверхность поддерживается во всех точках При постоянной температуре 1С.
За счет влияния температуры на вязкость профиль скорости можно считать плоским, как и в потоке поршня.Потому что ширина канала намного больше высоты、 Передача тепла к вертикальной стене незначительна.Продольная теплопроводность также пренебрежимо мала, а теплофизические параметры жидкости можно считать постоянными.Замкнутый Формула для средней температуры (температуры смешивания) жидкости по размерам канала, физическим свойствам жидкости и расстоянию x от канала. inlet.It необходимо отметить сходство между этим Задачи и примеры 21.
Смотрите также:
| Теплообмен при ламинарном движении | Теплообмен при турбулентном движении. Входные эффекты |
| Теплообмен при развивающемся профиле скорости | Аналогия между переносом импульса и тепла |

