Оглавление:



Построение эпюр внутренних усилий в балках и плоских стержневых системах при прямом изгибе
Прямой изгиб стержня происходит, когда нагрузка, приложенная к стержню, перпендикулярна оси (боковая нагрузка), действующая от главной центральной плоскости инерции, и чаще всего происходит на симметричной плоскости стержня. Статический расчет стержня при прямом изгибе осуществляется на рабочей поверхности поперечной нагрузки (силовой плоскости).
- Прямой стержень, который работает в основном Избибе, обычно называют балкой. В прямом поперечном сечении балки при прямом изгибе может действовать сила внутренней силы-поперечная сила С =и изгибающий момент (рис. 5.1).
Если все нагрузки, действующие на балку, включая опорную заднюю Яшину, неизвестны, то внутренние силы можно определить статически с помощью секционного метода. Людмила Фирмаль
Боковая сила любого участка белка определяется как сумма Проекция всех нагрузок, приложенных к одной из 1-х частей белков, на нормали осей этого сечения. Боковая сила считается положительной, если она стремится повернуть остальную часть балки вдоль прямой стрелки относительно центра тяжести сечения (рис. 5.2).
Изгибающий момент любого участка балки определяется как S ^ мм момента всех нагрузок, приложенных к любой части балки относительно центра тяжести конкретного участка. При расчете балки МС〜, изгибающий момент считается положительным, если он вызывает удлинение нижних волокон балки(рис. 5.3). Внутренние силы обычно изменяются по длине балки.
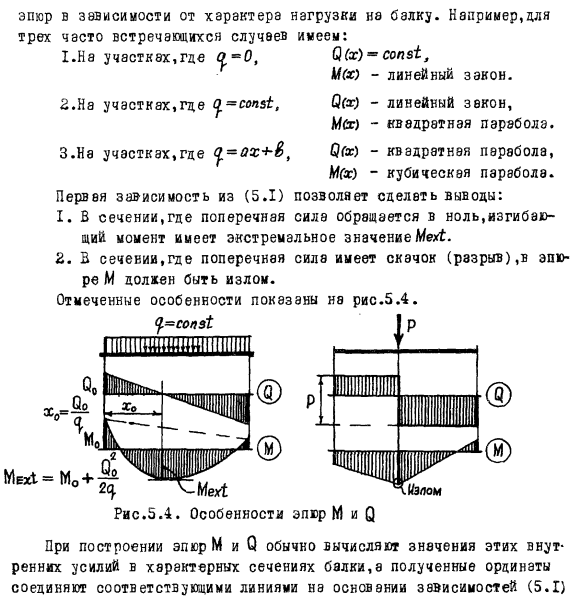
- Законы их изменения графически изображены с помощью диаграмм M и 0.При построении графика изгибающего момента мы обычно откладываем м-координату растянутых волокон. Рисунок в зависимости от характера нагрузки на балку.
Например, для 3 часто встречающихся случаев: 0 (x)= co $ 1, M (x) — линейный закон. 1. В области ^ = 0、 ^ = в области строительства, 3.В области = d (x) — линейный закон, Mst) — квадратная парабола. YGh) — квадратная парабола, MSx) — кубическая парабола.
Первая зависимость из (5.1) завершается: 1.In на участках, где отсутствует боковая сила, изгибающий момент имеет экстремальное значение MeL. 2.In сечение, где происходит скачок (разрыв) к боковой силе, м будет изломом фигуры. Людмила Фирмаль
При построении графиков м и 0 значения этих внутренних сил обычно вычисляются в характеристическом сечении балки, а полученная ордината соединяется с соответствующими линиями на основе зависимостей.
Смотрите также:
Предмет сопротивление материалов: сопромат
| Напряженное и деформированное состояния в точке | Напряженное состояние в балках при прямом изгибе и расчеты на прочность |
| Кручение стержней | Статически неопределенные задачи |

