

Тип работы: Задача
Предмет: Сопротивление материалов
Статус: Выполнен
Год работы: 2020
Страниц: 1
Оригинальность: 97% (antiplagiat.ru)
Формат: Скан (Рукопись)
Цена: 291 руб.
Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
Благодаря этой странице вы научитесь сами решать такие задачи:
Помощь по сопромату и решение задач на заказ
Другие похожие задачи:
| Задача 1.30. При установке жесткой балки | Задача 2.2 Стальная полоса прямоугольного сечения |
| Задача 1.31. Для конструкции требуется определить | Задача 2.3 Стальной прокатный двутавр |
Описание работы:
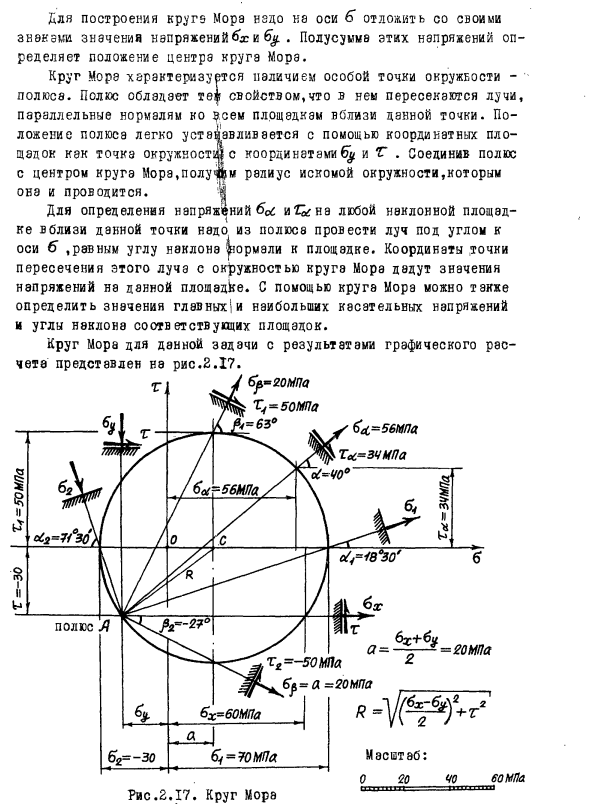
Задача 2.1 На координатных площадках вблизи данной точки тела,находящегося в условиях плоского напряженного состояния,действуют напряжения 6х=60 МПа, бу = -20МПа, Тих■Т=-30МПа. Направления действия этих напряжений ± с учетом знаков показаны на рис.2.14 для бесконечно малого элемента с координатными площадками. Требуется определить аналитически и графически:1. Значения главных напряжений и углы наклона главных площадок.2.Значения наибольших касательных напряжений и углы наклона площадок, где они действуют. 3. Значения нормальных и касательных напряжений на площадке с углом наклона нормали к оси х, равным d=4О°. Вычисляем значения главных напряжений по формуле (2.13): 6-Vj2= е0Н-20) ±-\J(6Q-H0)p = 20±so. 6а: =60 МПа Т=30МПа Рис.2.14.Напряжения на координатных площадках 6J=6/mx — 70 МПа, Положение главных площадок: Т -30 Рис.2.15.Гл.площадки 70МПа =4=18°2б’ Положение главных площадок вблизи данной точки показано на рис.2.15. Проверяем правильность вычислений: 6> б2 = 70+(-30) = бх+б# =60 + (-20) =40 МП а , Наибольшие .касательные напряжения вблизи данной точки равны: Определяем положение площадок с наи- 4 — — большими касательными напряжениями: = 2(Т<2-Т) _ 2 [±50-(-30)] бх-fy 60-(-20) Рис.2.16.Площадки с Проверяем правильность вычислении: Последняя проверка показывает»что площадки с наибольшими касательными напряжениями наклонены под углом 45°к главным площадкам Нормальные напряжения на площадках с наибольшими касательными напряжениями равны 60+(-2о) bp = ^ J = ——- =2оша. Определяем по формулам (2.12) значения напряжений на площадке, нормаль к которой наклонена к оси х под углом Для графического исследования напряженного состояния вблизи данной точки приведем формулы (2.12) к следующему виду: 6х+6ц* * * (2.23) Уравнение (2,23) можно рассматривать как уравнение окружности в осях 6″ и Г с центром на горизонтальной оси 6 . Эта окружность называется кругом Мора для плоского напряженного состояния. Для построения круга Мора надо на оси 6″ отложить со своими знаками значения напряжений бх и б у . Полусумма этих напряжений определяет положение центра круга Мора. Круг Мора характеризуется наличием особой точки окружности -полюса. Полюс обладает тем свойством,что в нем пересекаются лучи, параллельные нормалям ко всем площадкам вблизи данной точки. Положение полюса легко устанавливается с помощью координатных площадок как точка окружности с координатами и Т . Соединив полюс с центром круга Мора,получим радиус искомой окружности,которым она и проводится. Для определения напряжений бос и Т* на любой наклонной площадке вблизи данной точки надо из полюсе провести луч под углом к оси б ,равным углу наклона нормали к площадке. Координаты точки пересечения этого луча с окружностью круга Мора дадут значения напряжений на данной площадке. С помощью круга Мора можно также определить значения главных’и наибольших касательных напряжений и углы наклона соответствующих площадок. Круг Мора для данной задачи с результатами графического расчета представлен на рис.2.17.
