






- Представленные уравнения нестационарной теплопроводности являются дифференциальными в частных производных для решения такого уравнения существует 2 общих метода: метод «разделения переменных» и метод использования интегральных преобразований(обычно преобразование Лапласа). Оба этих метода могут быть использованы для получения решений более простых уравнений. Однако для более сложных задач более уместно преобразование Лапласа. Метод разделения переменных показан в примере 21.2. Читатель, который имеет ограниченные знания в области дифференциальных уравнений может следовать.
Метод преобразования Лапласа является более сложным, поэтому он не объясняется. Пример 21. Два Резиновый лист толщиной 12,7 мм следует отверждать при температуре 144,4°с в течение 50 минут. Если начальная температура листа составляет 22°C, и обе поверхности нагреваются, найдите время, необходимое для температуры 1. Как решить уравнение теплопроводности описано в большинстве руководств по применению математики в технике. Вы можете порекомендовать 3 книги(113, 174, 22]. Каучук считается равным 0,00026 Л2 / ч. одномерная теплота Середина листа достигала 143,3°C.
Как только начинается вулканизация, мы можем предположить, что температура поверхности установлена на 144,4°C и поддерживается на этом уровне на протяжении всего процесса. Температуропроводность- Дифференциальное уравнение нестационарного влагосодержания(21. 1) формат является: 0 / _ х дх ДХ Диу dx2 Как показано на рисунке, начало координат выбрано в середине листа, поэтому x-это расстояние от центра. 21. 1, а x0-половина толщины. При решении уравнений в частных производных обычно полезно определять переменные, поскольку они изменяются от нуля до нуля или от нуля до бесконечности в безразмерном порядке.
Отсюда и выражение (21. 2) пишите. 144.4-Х ХВ 144.4-22″х0」 Формула(21. Два) дю _ d2U 00 ″» дп2 ’ За (1) (2) (2) Вы можете проверить, назначив новую переменную и выполнив указанное дифференцирование. Решение уравнения (2) получено в предположении, что такое решение может быть описано как 2 члена. ШЧ.’С Ц х-0 х-ХV рис.21. 1.Нестационарная теплопроводность резиновых листов (например, 21.2). В виде произведения (4 )) (5) г = влг (3) Где 6-функция только 0, где время-переменная, и N-функция только n, где расстояние-переменная.
Если V-это решение, если мы дифференцируем V в соответствии с (2)、 00 _0_0 ^ _- Уравнение может быть преобразовано так, что только члены, зависящие от 0, находятся слева, и только те, которые зависят от n, находятся справа. 1 00 __ 1 02 ^ 0 ’00 N’DP * * Потому что время и расстояние в этой задаче не зависят друг от друга、 Левая часть этого уравнения не зависит от расстояния, а правая-от времени. Поэтому каждый из них должен быть постоянным. Для удобства эта константа представлена в виде-a2.Тогда вы можете написать 2 обыкновенных дифференциальных уравнения 1г + » 2С = ° (6) решение уравнения (6) имеет простую форму: с = С1Е-а ’ 8.
Читатель, знакомый с дифференциальными уравнениями, узнает нормальное дифференциальное уравнение 2-го порядка с постоянным коэффициентом в Формуле (7).Его решение записано следующим образом. Ту = C2z1n АП + С3, потому что АП. (9 )) После получения выражений 0 и AG можно записать решение уравнения в частных производных, которое вы искали в виде следующего (3) М = ЭМ = АР Е » А * Е (С2 КТ АП + С9 потому что АП).(10 )) Уравнение содержит 4 константы СсС2, С3 и А. Однако C1 может быть объединен с C1 и C8, поэтому для определения решения требуются только следующие 3 дополнительных условия x: 1.Поскольку система симметрична, то нет потока тепла через центральную линию (x = 0).
Итак, если= 0 и n = 0. 2.Поверхность (x = X0 = 1.27.In 10 ″ 1 2), температура всегда постоянна (144,4°C). таким образом, для n-1 Y = 0. 3.Первый(t = 0), температура всего листа составляет 22°C. So, 0 = 0 и Y = 1. Во-первых, используйте граничное условие 1. =11е’а * 0(АП-СЗА СГА, потому что ЗТ ЗС). если η= 0, ntap = 0、 Созап= 1.So … Для того чтобы эта формула соответствовала общему решению и была равна нулю, коэффициент Cr должен быть равен нулю.
После такого упрощения общее решение можно описать следующим образом: 9soz АП’, г = е-0 (я) C1u и C9 включены в A. Используйте граничное условие 2. 0 = а e_a * 9 потому что. л Зия Этому условию соответствует множество значений типа -. присвоение 1 из этих значений a выражению (I) удовлетворяет требованиям 2-го граничного условия. Однако, Косинус 1. автор называет эти условия граничными (Лобягу). Она соответствует терминам, принятым в русской литературе.
Невозможно представить себе какое-либо распределение температуры в пластине (заметьте, трансформаторе).в то же время любая функция может быть представлена в виде бесконечного ряда косинусов, если члены ряда взяты соответствующими коэффициентами. Поэтому типичное решение может быть записано в следующем формате: Т-L1е 4, потому что-Н + L2e, потому что —-— 4 сентября. 4-я » е>• 2. Один потому что (24-1) Япп Два (12) 4-это целое число.
- С помощью дифференцирования и подстановки можно увидеть, что эта сумма удовлетворяет предыдущим уравнениям в частных производных и первому граничному условию * 2. Последним шагом является определение констант, которые выступают в качестве коэффициентов членов этого ряда. Это делается с использованием начальных условий. Формула(12) это хорошая вещь. Да. Платформа деятельности zlp ,. 。 (21-1) ЛВ… 1 = Alcoz — + AgCO $ — p. 。 。 4-Л {Созь-. (13 )) Умножьте обе стороны этого уравнения на cos. (24-1) Япп Два 1N и целое Он летит в диапазоне 0-1.Левая часть-это Интегрирование первого члена справа может быть вычислено с помощью интегральной таблицы.
У нас есть этот интеграл равен нулю для всех значений целого числа 4, за исключением unity. So, 2-й член справа исчезнет, и все последующие члены, кроме 4-го, также исчезнут. Этот член является ■Мне 21-1 −2 ~ ~ 2〜 ___ 1.(Р 24-1-п \ −4- 24-1 л \ 2 2° / 2 * Таким образом, формула (13) имеет вид、 2 _1_ (__4 в- 24-1 I {2 * здесь { 4 (-1)* I(2″ −1)» Т. Д.) (То есть, a-I, L2-ZA, L3-5A и Так что есть общее решение г =±е ’ (^’, потому что ^ 4-Т2″ 5″ » + _e / Кос-. Формат выражения (14), написанного в сжатой форме, является (21-1) Л 12 (14) (21-1) ЛВ Два (15 )) Теперь применим формулу (15) к рассматриваемому конкретному случаю. Так… — (?■ * _l, за.- Т. СИА.
Это уравнение должно быть решено относительно 0 (включая переменное время t) методом проб и ошибок. Рассмотрим только первый член справа в качестве первого приближения. Дай ’^»^090 = 2.0!; ми|(-= ) Т = 0.313 Н18. 7 млн Чтобы убедиться, что все члены, кроме первого, пренебрежимо малы, следует проверить относительную величину членов ряда, представляющих решение. Если = 2.01, то строка принимает следующий вид: u-Ai-’>«_______ А-Е «44′ 8-!— е » 124. Г»я зя 5л Подгонка подгонки очевидна, где используется только первый член расширения. Не все решения в рядах сходятся так быстро, но во многих случаях.
Обычно это можно установить по типу индикатора членов ряда (как в данном случае). Температуру в любой точке резинового листа можно определить в данный момент, подставив значения Р и 0, соответствующие формуле (15). 21. 1 был отредактирован, чтобы показать расширение температурного профиля во время нагрева. Очевидно, что результаты на поверхности в нулевое время противоречивы.
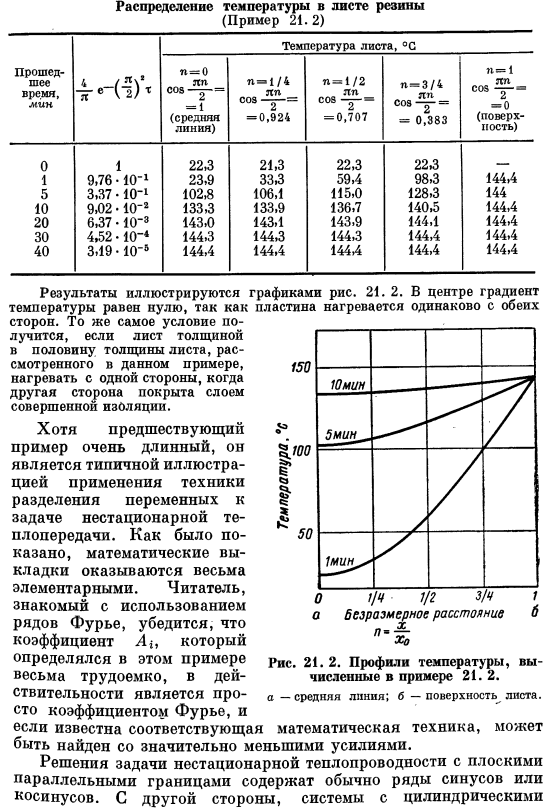
Это является результатом условий, наложенных на распределение температуры раствора резинового листа(пример 21.2) Затраченное время, минимальная температура листьев,°С н = 0 ЛП-008-= 1 (средняя линия) и N = 1/4 ПЛ сов — ^ — = 0.924 Н = 1/2 ЛП потому что — = = 0.707 Н = 3/4 ПЛ с — = 0.383 П= 1ЯП003 — = = 0 (поверхность) 0 1 22.3 21.3 22.3 223 __ 1 9.76•10’1 23.9 33.3 59.4 98.3 144.4 5 3.37•10 «1 102.8 106.1 115.0 128.3 144 10 9.02 −10’2 133.3 133.9 136.7 140.5 144.4 20 6.37•10’3 143.0 143.1 143.9 144.1 144.4 30 4.52-10- * 144.3 144.3 144.3 1444 1444 40 3.19 * 10 «a 144.4 144.4 1444 1444 144.4 Результат показан на графике рисунка. 21.
Обе стороны пластины нагреваются равномерно, так что температурный градиент равен нулю. Когда одна сторона листа в половину толщины листа, рассматриваемого в данном примере, покрыта полным теплоизоляционным слоем, она останется такой же при нагревании с одной стороны. Приведенный выше пример является очень длинным, но это типичный пример применения метода разделения переменных к задаче нестационарного нагрева transfer. As показано, что математические расчеты очень рудиментарны. Читатели, знакомые с использованием рядов Фурье, коэффициент а、 Вы.- Рис. 21.2.Температурный профиль, численное значение примера 21 2. А-средняя линия; Б-поверхность листа.
Это очень хлопотно определить в данном примере, если на практике это просто коэффициент Фурье, а соответствующая математическая техника известна、 Его находят с гораздо меньшими усилиями. Решения задачи нестационарной теплопроводности с плоскими параллельными границами обычно включают ряд синусоидальных или косинусоидальных волн. Система с цилиндрическими границами, с другой стороны, приводит к выражению, известному как функция Бесселя. Существует таблица этих функций[45, 72]. Если цилиндр достаточно долго для устранения конечного эффекта нагревается с поверхности, находящейся при постоянной температуре, то координаты температуры, времени и радиуса вычисляются по формуле 21.
Производное от дифференциального уравнения связано с ним. d1_ _ х /. Один \ ДХ-ОКП \ почтовый индекс dg2 \ Р)* (21.4) Из этой формулы, пример 21. Если вы идете как 2, Вы получаете 2 решения.1-экспоненциальная функция времени, а другая 1-функция Бесселя, содержащая текущий радиус. После объединения 1 из этих решений решение о выполнении граничных условий принимается в следующем виде: Много = 2 ^ ы(о ^ о• (21.5) 7°и / 1 — функции Бесселя класса 1 (0 порядка и 1 порядка соответственно), а ax-равновесие 7°(a {7?) = 0 / — корень. Начальная температура 2°, температура поверхности (постоянная) и радиус цилиндра B.
Для многих распространенных задач теплопроводности решение представлено в виде графика 2.При рассмотрении этих графиков одни и те же (безразмерные) переменные отличаются от переменных, используемых в приведенном выше решении. Нормально отрегулировать Текущее относительное изменение температуры В абсциссе индикатор откладывается, а его время включается в качестве переменной. Пространственная переменная n функционирует как параметр для кривых 1 семейства каждого графика, а семейства каждой кривой различаются граничными условиями, то есть имеет ли поверхность конвективное сопротивление (выраженное в коэффициенте теплопередачи a) или является ПЭТ.
Пример 21. Три Пример использования Perry 21. Найдите решение задачи 2(стр. 462, Рис. 4).Используя нотацию справочника Перри、 Год= 0,00026 0.6352 * 10 «4 1 тонна Frgt = 6,44 Т; 144.4-143.3 144.4-22 = 0.0090; М = — — — = 0; н = = 0. ATGT GT 1 точнее, умножим сумму данного решения на константу и определим дальше от начальных условий. (Примечание, редактировать) 2 Perry, p. см. 462.It предполагается, что температура поверхности постоянна.
Смотрите также:
| Полый цилиндр. Многослойный цилиндр | Правило Ньюмена |
| Нестационарная теплопроводность. Основные уравнения | Численные, графические и аналоговые методы в исследовании теплопроводности |
