Оглавление:

Прежде чем изучать готовые решения задач по атому и атомному ядру, нужно знать теорию, поэтому для вас я подготовила краткую теорию по разделу «атом и атомное ядро в физике», и примеры решения в которых подробно решены задачи.
Эта страница подготовлена для школьников и студентов.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Атом и атомное ядро. Определения, понятия и законы
Опыты Резерфорда по рассеянию α — частиц. Планетарная модель атома
К началу XX века было убедительно показано, что электрон является одной из составных частиц любого вещества. Из классической электромагнитной теории следовало, что размеры электрона не превышают 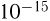 м (по современным данным — не более
м (по современным данным — не более 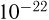 м). Кинетическая теория 19-го столетия показала, что размеры атомов имеют порядок
м). Кинетическая теория 19-го столетия показала, что размеры атомов имеют порядок  м. Учитывая это, Дж. Дж. Томсон в 1903 году предложил модель, согласно которой атом содержит электроны, которые вкраплены в положительно заряженную среду, заполняющую весь объем атома, масса которой составляет большую часть его массы, а ее заряд нейтрализует суммарный заряд электронов.
м. Учитывая это, Дж. Дж. Томсон в 1903 году предложил модель, согласно которой атом содержит электроны, которые вкраплены в положительно заряженную среду, заполняющую весь объем атома, масса которой составляет большую часть его массы, а ее заряд нейтрализует суммарный заряд электронов.
Однако уже в 1911 году Эрнест Резерфорд опытным путем доказал, что эта модель несостоятельна. Им были проведены эксперименты по рассеянию 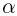 — лучей. (
— лучей. (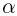 — лучи представляют собой поток
— лучи представляют собой поток 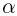 — частиц. т.е. дважды ионизованных атомов гелия, имеющих положительный заряд, равный
— частиц. т.е. дважды ионизованных атомов гелия, имеющих положительный заряд, равный 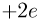 , и возникающих в результате радиоактивного распада (см. ниже)). Э. Резерфорд с помощью свинцового коллиматора выделял узкий пучок
, и возникающих в результате радиоактивного распада (см. ниже)). Э. Резерфорд с помощью свинцового коллиматора выделял узкий пучок 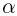 — лучей и пропускал их через очень тонкую золотую фольгу. Регистрировались
— лучей и пропускал их через очень тонкую золотую фольгу. Регистрировались 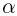 — частицы по вспышкам света на детекторе из сернистого цинка. Было установлено, что почти все
— частицы по вспышкам света на детекторе из сернистого цинка. Было установлено, что почти все 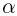 — частицы проходили сквозь фольгу, сохраняя прежнее направление движения или отклоняясь от него на очень малые углы. Однако некоторые
— частицы проходили сквозь фольгу, сохраняя прежнее направление движения или отклоняясь от него на очень малые углы. Однако некоторые 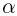 — частицы отклонялись на углы, превышающие 90°, т. е. они фактически двигались в обратном направлении. Если бы была справедлива модель атома Томсона, то такие события были бы невозможны в принципе:
— частицы отклонялись на углы, превышающие 90°, т. е. они фактически двигались в обратном направлении. Если бы была справедлива модель атома Томсона, то такие события были бы невозможны в принципе: 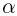 — частицы должны были бы свободно проходить сквозь атомы золота, и только некоторые из них могли слегка отклониться в кулоновском поле электронов. Результатом опытов Резерфорда явилась ядерная модель атома: в центре атома находится ядро, имеющее очень малый объем, в котором сосредоточен весь положительный заряд атома; остальную часть атома занимает облако электронов. Линейные размеры ядра составляют
— частицы должны были бы свободно проходить сквозь атомы золота, и только некоторые из них могли слегка отклониться в кулоновском поле электронов. Результатом опытов Резерфорда явилась ядерная модель атома: в центре атома находится ядро, имеющее очень малый объем, в котором сосредоточен весь положительный заряд атома; остальную часть атома занимает облако электронов. Линейные размеры ядра составляют 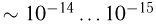 м. Практически вся масса атома сосредоточена в ядре.
м. Практически вся масса атома сосредоточена в ядре.
В этой модели опыты Резерфорда получили простое объяснение. Проходя сквозь электронную оболочку атома 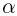 — частицы не должны испытывать заметного отклонения, поскольку масса электрона намного меньше массы
— частицы не должны испытывать заметного отклонения, поскольку масса электрона намного меньше массы 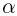 — частицы, а отрицательный заряд всех электронов распределен по всему объему атома. Однако те немногочисленные частицы, которые пролетают вблизи ядра, испытывают резкие отклонения. В этих опытах была также подтверждена справедливость закона Кулона для очень малых расстояний между зарядами.
— частицы, а отрицательный заряд всех электронов распределен по всему объему атома. Однако те немногочисленные частицы, которые пролетают вблизи ядра, испытывают резкие отклонения. В этих опытах была также подтверждена справедливость закона Кулона для очень малых расстояний между зарядами.
Электроны атома, чтобы не упасть на ядро под действием кулоновского притяжения, должны двигаться вокруг ядра по орбитам, подобно планетам, поскольку кулоновские и гравитационные силы одинаково зависят от расстояния. Поэтому модель атома Резерфорда называют планетарной. Однако вращающиеся вокруг ядра электроны, согласно классической электродинамике, должны испускать электромагнитные волны, теряя при этом свою энергию и постепенно приближаясь к ядру, т.е. атом не может быть устойчивым. Спектр излучаемых частот при этом должен быть непрерывным.
Еще в середине XIX века было установлено, что свечение различных газов (в пламени и в электрическом разряде) содержит участки спектра с четко выраженными дискретными линиями. Для частот 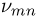 линейчатого спектра водорода была получена формула Бальмера-Ридберга:
линейчатого спектра водорода была получена формула Бальмера-Ридберга:
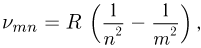
где 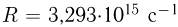 — постоянная Ридберга,
— постоянная Ридберга, 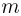 и
и 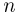 — целые числа, причем
— целые числа, причем 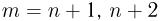 и т. д.
и т. д.
Квантовые постулаты Бора
Для объяснения наблюдаемых свойств атомов Нильс Бор в 1913 г. выдвинул два положения, называемые постулатами Бора:
- В атоме существуют дискретные стационарные состояния, каждому из которых соответствует определенная энергия
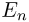 . При движении вокруг ядра электроны атома, находящегося в стационарном состоянии, не излучают электромагнитных волн.
. При движении вокруг ядра электроны атома, находящегося в стационарном состоянии, не излучают электромагнитных волн. - При переходе атома из одного стационарного состояния в другое испускается или поглощается один фотон. Энергия фотона равна разности энергий в двух его стационарных состояниях: hvmn
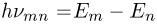 .
.
Испускание и поглощение энергии атомом
Если 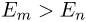 , то происходит излучение фотона, если же
, то происходит излучение фотона, если же 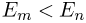 , то — поглощение фотона. Частота фотона
, то — поглощение фотона. Частота фотона 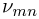 который испускается (поглощается) атомом, равна
который испускается (поглощается) атомом, равна 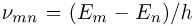 . Атом, находящийся в состоянии с наименьшей энергией, не может испустить фотон. Такое состояние атома называется основным, остальные состояния (с большей энергией) называются возбужденными.
. Атом, находящийся в состоянии с наименьшей энергией, не может испустить фотон. Такое состояние атома называется основным, остальные состояния (с большей энергией) называются возбужденными.
Для определения уровней энергии атома водорода Н. Бор предложил гипотезу о том, что в планетарной модели стационарными являются лишь те состояния, при которых момент импульса электрона, движущегося по круговой орбите, принимает дискретные значения:
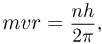
где 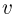 — скорость электрона,
— скорость электрона, 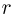 — радиус орбиты,
— радиус орбиты, 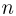 — натуральное число. Эта формула называется правилом квантования Бора для круговых орбит. Найденное с ее помощью выражение для частоты излучения полностью совпадает с (5.2).
— натуральное число. Эта формула называется правилом квантования Бора для круговых орбит. Найденное с ее помощью выражение для частоты излучения полностью совпадает с (5.2).
Развитая впоследствии квантовая механика естественным образом объясняет постулаты Бора и полностью описывает движение микрочастиц.
Непрерывный и линейчатый спектры. Спектральный анализ
Спектр излучения и поглощения вещества в газообразном состоянии всегда содержит участок, состоящий из узких дискретных линий, который называется линейчатым спектром, и участок, где распределение частот непрерывное (непрерывный спектр).
Линейчатый спектр у каждого химического элемента и у каждого сорта молекул индивидуален и отражает структуру уровней энергии именно данного вещества. Это обстоятельство используется для определения качественного и количественного состава вещества, т. е. для так называемого спектрального анализа. Для получения спектров излучения вещество возбуждают с помощью искрового, дугового или радиочастотного разряда, либо облучением светом от дополнительных источников: газоразрядных ламп, лазеров и т. д. Спектры поглощения получают, пропуская белый свет через исследуемое вещество. В этом случае на сплошном спектре появляются темные линии, обусловленные поглощением света в данном участке спектра.
Спектральный анализ отличается быстротой получения результатов и высокой чувствительностью.
Использование лазеров позволяет регистрировать даже единичные атомы или молекулы данного сорта.
Экспериментальные методы регистрации заряженных частиц
Для регистрации радиоактивных излучений используются приборы, основанные на ионизирующем или фотохимическом действии этих излучений.
Камера Вильсона — прибор для наблюдения следов (треков) заряженных частиц. Действие основано на конденсации пересыщенного пара на ионах, образующихся вдоль траектории заряженной частицы. Пересыщенный пар получается быстрым сжатием насыщенного пара воды или спирта, находящегося в стеклянном цилиндре. Частицы могут либо испускаться источником, помещенным внутри камеры, либо попадать в нее извне. Треки фотографируются несколькими фотоаппаратами для получения стереоскопического изображения. Природу и свойства частиц можно определить по длине ее пробега и импульсу, измеряемому по искривлению траекторий частиц в магнитном поле, в которое помещается камера Вильсона.
Пузырьковая камера — прибор для регистрации следов (треков) заряженных частиц высоких энергий. Действие основано на вскипании перегретой жидкости вблизи траектории частицы. Очень чистую жидкость можно нагреть выше точки кипения, но такая жидкость нестабильна. Прохождение заряженной частицы через перегретую жидкость приводит к образованию вдоль следа частицы «зародышевых» центров кипения, которые возникают вследствие ионизации атомов или молекул, входящих в состав жидкости. За время порядка миллисекунды образующиеся пузырьки достигают размеров порядка 50 — 300 мкм и могут быть сфотографированы.
Счетчик Гейгера — газоразрядный прибор, срабатывающий при прохождении через его рабочий объем заряженных частиц. Счетчик состоит из стеклянной трубки, покрытой внутри металлическим слоем (катод), и тонкой металлической нити, идущей вдоль оси трубки (анод). Трубка заполняется газом, например, аргоном. К электродам прикладывается напряжение в несколько сотен вольт. Заряженная частица, пролетая через газ, вырывает из атомов электроны. Электрическое поле между анодом и катодом ускоряет свободные электроны до энергий, при которых они способны ионизировать атомы. Возникает лавина ионов и электронов, и ток между электродами возрастает, что и регистрируется электронной схемой. Величина сигнала (импульса тока) не зависит от энергии частиц, поэтому прибор работает как счетчик заряженных частиц.
Фотоэмульсионный метод основан на применении толстослойных фоточувствительных покрытий. Фотоэмульсия содержит большое количество микроскопических кристалликов бромида серебра. Быстрая заряженная частица, проходя через кристаллики, отрывает электроны от отдельных атомов брома. Цепочка таких кристалликов образует скрытое изображение. При проявлении восстанавливается металлическое серебро и трек частицы становится видимым. По длине и толщине трека можно оценить энергию и массу частицы.
Состав ядра атома. Изотопы
Ядро атома любого химического элемента состоит из 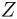 положительно заряженных протонов и
положительно заряженных протонов и 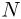 не имеющих электрического заряда нейтронов. Заряд протона по абсолютной величине равен заряду электрона. Протон и нейтрон являются двумя зарядовыми состояниями ядерной частицы, которая называется нуклоном. Количество протонов в ядре
не имеющих электрического заряда нейтронов. Заряд протона по абсолютной величине равен заряду электрона. Протон и нейтрон являются двумя зарядовыми состояниями ядерной частицы, которая называется нуклоном. Количество протонов в ядре 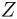 совпадает с атомным номером соответствующего химического элемента в периодической системе Менделеева. Заряд ядра равен
совпадает с атомным номером соответствующего химического элемента в периодической системе Менделеева. Заряд ядра равен 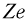 .
.
Массовым числом ядра 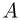 называется общее число нуклонов в ядре
называется общее число нуклонов в ядре 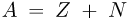 . Для обозначения ядра данного химического элемента
. Для обозначения ядра данного химического элемента 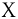 используется символ
используется символ 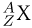 . Ядра с одним и тем же зарядом
. Ядра с одним и тем же зарядом 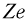 , но с разными
, но с разными 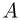 , называются изотопами. Изотопы ядер данного химического элемента отличаются числом нейтронов
, называются изотопами. Изотопы ядер данного химического элемента отличаются числом нейтронов 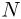 . Примеры: изотопы водорода
. Примеры: изотопы водорода 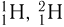 (или
(или 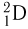 — дейтерий),
— дейтерий), 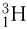 (или
(или 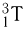 — тритий); изотопы урана
— тритий); изотопы урана 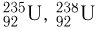 .
.
Масса атома практически совпадает с массой его ядра, поскольку масса электрона 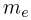 составляет всего 1/1836 от массы протона
составляет всего 1/1836 от массы протона 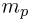 и 1/1840 от массы нейтрона
и 1/1840 от массы нейтрона 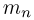 (нейтрон несколько тяжелее протона). В атомной и ядерной физике широко используется атомная единица массы — а. е. м., которая равна 1/12 массы ядра углерода
(нейтрон несколько тяжелее протона). В атомной и ядерной физике широко используется атомная единица массы — а. е. м., которая равна 1/12 массы ядра углерода 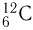 , что составляет
, что составляет 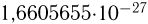 кг.
кг.
Нуклоны, т. е. протоны и нейтроны, в ядре связаны между собой ядерными силами, которые намного превышают силу кулоновского отталкивания между протонами (отсюда название — сильные взаимодействия). Ядерные силы действуют только на расстояниях порядка 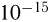 м.
м.
В атомной и ядерной физике для измерения энергии широко используется внесистемная единица электрон-вольт 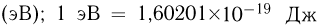 . В ядерной физике энергия часто измеряется также в мегаэлектрон — вольтах
. В ядерной физике энергия часто измеряется также в мегаэлектрон — вольтах 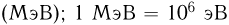 .
.
Энергия связи атомного ядра 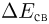 по абсолютной величине равна работе, которую надо совершить для расщепления ядра на составляющие его нуклоны без сообщения им кинетической энергии. Из закона сохранения энергии следует, что при образовании ядра из свободных нуклонов должна выделиться энергия, равная
по абсолютной величине равна работе, которую надо совершить для расщепления ядра на составляющие его нуклоны без сообщения им кинетической энергии. Из закона сохранения энергии следует, что при образовании ядра из свободных нуклонов должна выделиться энергия, равная 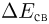 . Удельной энергией связи ядра
. Удельной энергией связи ядра 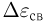 называется величина
называется величина 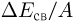 , равная средней энергии связи, приходящейся на один нуклон.
, равная средней энергии связи, приходящейся на один нуклон.
Мерой энергии связи атомного ядра является дефект массы. Дефектом массы 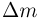 называется разность между суммарной массой всех нуклонов ядра в свободном состоянии и массой ядра
называется разность между суммарной массой всех нуклонов ядра в свободном состоянии и массой ядра 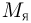 :
:
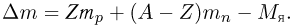
Согласно теории относительности, энергия связи данного ядра и его дефект массы связаны соотношением: 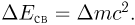
Понятие о ядерных реакциях
Ядерными реакциями называются превращения атомных ядер, вызванные их взаимодействием с различными частицами или друг с другом. В большинстве случаев в ядерных реакциях участвуют два ядра и две частицы. Символическая запись ядерной реакции: 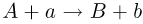 , где
, где 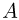 и
и 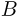 — исходное и конечное ядра,
— исходное и конечное ядра, 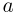 и
и 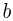 — исходная и конечная частицы в реакции. Исторически первой была наблюдена ядерная реакция превращения азота под действием
— исходная и конечная частицы в реакции. Исторически первой была наблюдена ядерная реакция превращения азота под действием 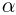 — частиц в кислород:
— частиц в кислород: 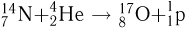 . При всех ядерных реакциях соблюдаются законы сохранения электрического заряда и числа нуклонов.
. При всех ядерных реакциях соблюдаются законы сохранения электрического заряда и числа нуклонов.
Радиоактивность. Виды радиоактивных излучений и их свойства
Радиоактивность — способность некоторых атомных ядер самопроизвольно превращаться в другие ядра с испусканием частиц. Естественная радиоактивность, как правило, наблюдается у тяжелых ядер. Радиоактивное превращение сопровождается испусканием 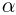 — частиц,
— частиц, 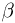 — частиц, а также очень коротковолнового электромагнитного излучения (
— частиц, а также очень коротковолнового электромагнитного излучения (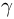 — излучения). Состав
— излучения). Состав 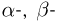 и
и 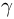 — излучений установлен по их отклонению в магнитном поле. Известно, что
— излучений установлен по их отклонению в магнитном поле. Известно, что 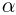 — лучи представляют собой поток ядер гелия,
— лучи представляют собой поток ядер гелия, 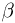 — лучи — поток быстрых электронов. Превращения атомных ядер, которые сопровождаются испусканием
— лучи — поток быстрых электронов. Превращения атомных ядер, которые сопровождаются испусканием 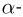 и
и 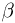 — частиц, называются соответственно
— частиц, называются соответственно 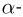 и
и 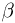 — распадом.
— распадом.
Большинство встречающихся в природе ядер устойчиво. Однако при значениях массовых чисел вблизи 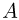 = 210 ядра перестают быть устойчивыми. Это в первую очередь объясняется близкодействующим характером ядерных сил: силы ядерного притяжения действуют только между данным нуклоном и его непосредственными соседями. Вместе с тем, так как кулоновские силы дальнодействующие, между данным протоном и всеми остальными протонами в ядре действует кулоновское отталкивание. Для ядер с достаточно большими атомными номерами кулоновское отталкивание может превысить ядерное притяжение. Действительно, не существует устойчивых ядер с
= 210 ядра перестают быть устойчивыми. Это в первую очередь объясняется близкодействующим характером ядерных сил: силы ядерного притяжения действуют только между данным нуклоном и его непосредственными соседями. Вместе с тем, так как кулоновские силы дальнодействующие, между данным протоном и всеми остальными протонами в ядре действует кулоновское отталкивание. Для ядер с достаточно большими атомными номерами кулоновское отталкивание может превысить ядерное притяжение. Действительно, не существует устойчивых ядер с 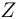 > 83.
> 83.
Цепные ядерные реакции
Ядра урана и ряда трансурановых элементов способны к реакциям деления ядра, при которых ядра, возбужденные захватом нейтрона, распадаются на две части, называемые осколками. При этом возможно высвобождение некоторого количества нейтронов. Деление тяжелого ядра сопровождается выделением огромной энергии. Например, при делении ядер, содержащихся в 1 г урана 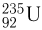 , выделяется энергия порядка
, выделяется энергия порядка 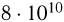 Дж. (Удельная теплота сгорания нефти, равная
Дж. (Удельная теплота сгорания нефти, равная 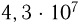 Дж/кг, примерно в два миллиона раз меньше!) В каждом акте деления, помимо осколков, возникают несколько
Дж/кг, примерно в два миллиона раз меньше!) В каждом акте деления, помимо осколков, возникают несколько 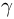 — квантов и в среднем 2,5 нейтрона. Если эти нейтроны вызывают другие акты деления, то возникает процесс самоподдерживающийся процесс цепной ядерной реакции. Цепные ядерные реакции используются в ядерных реакторах для получения энергии, а также в ядерном оружии.
— квантов и в среднем 2,5 нейтрона. Если эти нейтроны вызывают другие акты деления, то возникает процесс самоподдерживающийся процесс цепной ядерной реакции. Цепные ядерные реакции используются в ядерных реакторах для получения энергии, а также в ядерном оружии.
Термоядерная реакция
Выделение ядерной энергии возможно также в реакциях синтеза (слияния) легких ядер. Для осуществления такой реакции необходимо преодолеть кулоновские силы отталкивания между ядрами, что возможно при достаточно больших скоростях сталкивающихся частиц. Так, синтез гелия из легкого изотопа водорода происходит при температуре около 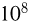 К, а для синтеза гелия из дейтерия и трития по схеме
К, а для синтеза гелия из дейтерия и трития по схеме 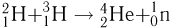 требуются температуры порядка
требуются температуры порядка 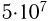 К. Поэтому такие реакции называются термоядерными. При синтезе 1 г гелия из дейтерия и трития выделяется энергия
К. Поэтому такие реакции называются термоядерными. При синтезе 1 г гелия из дейтерия и трития выделяется энергия 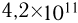 Дж. Управляемые термоядерные реакции представляют большой интерес для энергетики будущего.
Дж. Управляемые термоядерные реакции представляют большой интерес для энергетики будущего.
Биологическое действие радиоактивных излучений. Защита от радиации
Излучения радиоактивных веществ оказывают сильное воздействие на все живые организмы. Даже слабые излучения способны нанести существенные повреждения живым клеткам и вызвать опасные заболевания (лучевая болезнь). Механизм поражающего действия излучений на биологические объекты заключается в основном в ионизации атомов и молекул, что приводит к изменению их химической активности. В результате облучения в тканях образуются свободные радикалы, подавляющие действие ферментов, происходит разрыв хромосом, увеличивается число мутаций. Наиболее чувствительны к излучениям ядра клеток, особенно тех, которые быстро делятся.
Поэтому у человека излучения в первую очередь поражают костный мозг, из-за чего нарушается процесс образования крови.
Степень облучения связана с энергией поглощенного излучения. В СИ единицей поглощенной дозы является грэй (Гр). Доза в 1 Гр означает, что облученному веществу массой I кг передана энергия ионизирующего излучения I Дж.
Методы защиты от облучения: удаление от источников излучения; ограничение времени пребывания на загрязненной местности или вблизи радиоактивных источников; ограждение радиоактивных источников специальными экранами. К защитным мерам относится также дозиметрический контроль окружающей среды и продуктов питания.
Примеры решения задач
Задача №6.15.
Спираль, сопротивление которой 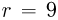 Ом, помещена в замкнутый сосуд. Сосуд содержит идеальный одноатомный газ, который занимает объём
Ом, помещена в замкнутый сосуд. Сосуд содержит идеальный одноатомный газ, который занимает объём 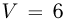 л. В течение времени
л. В течение времени 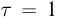 мин по спирали пропускали постоянный ток, после чего давление возросло на величину
мин по спирали пропускали постоянный ток, после чего давление возросло на величину 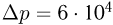 Па. Найти силу тока
Па. Найти силу тока 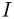 .
.
Решение:
По закону Джоуля-Ленца количество теплоты, выделяющееся в спирали за время 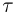 , равно
, равно 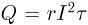 . Эта теплота идет на нагрев газа, происходящий при постоянном объеме:
. Эта теплота идет на нагрев газа, происходящий при постоянном объеме: 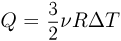 , где
, где 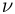 — количество газа,
— количество газа, 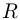 — универсальная газовая постоянная,
— универсальная газовая постоянная, 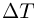 — изменение температуры газа. Из уравнения изохорного процесса следует, что
— изменение температуры газа. Из уравнения изохорного процесса следует, что 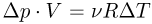 . Объединяя записанные выражения, получаем ответ:
. Объединяя записанные выражения, получаем ответ: 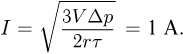
Задача №6.16.
Лазер излучает световые импульсы с энергией  Дж. Частота повторения импульсов
Дж. Частота повторения импульсов 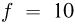 Гц. Коэффициент полезного действия лазера, определяемый как отношение излучаемой энергии к потребляемой, составляет
Гц. Коэффициент полезного действия лазера, определяемый как отношение излучаемой энергии к потребляемой, составляет 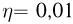 . Какой объем воды
. Какой объем воды 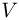 нужно пропустить за время
нужно пропустить за время 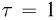 час через охлаждающую систему лазера, чтобы вода нагрелась не более, чем на
час через охлаждающую систему лазера, чтобы вода нагрелась не более, чем на 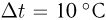 ? Удельная теплоемкость воды
? Удельная теплоемкость воды 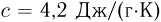 , плотность воды
, плотность воды 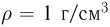 .
.
Решение:
Мощность излучения лазера равна произведению энергии одного импульса на частоту повторения: 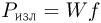 . Потребляемая лазером мощность по определению КПД есть
. Потребляемая лазером мощность по определению КПД есть 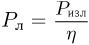 . Следовательно, мощность, которая должна быть отведена от лазера с помощью системы охлаждения, составляет величину
. Следовательно, мощность, которая должна быть отведена от лазера с помощью системы охлаждения, составляет величину 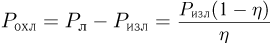
Количества тепла, отводимое системой охлаждения за время 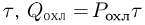 может быть выражено с использованием уравнения теплового баланса как
может быть выражено с использованием уравнения теплового баланса как 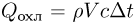 . Объединяя записанные соотношения, получаем ответ:
. Объединяя записанные соотношения, получаем ответ: 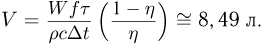
Задача №6.17.
Тепловая машина с максимально возможным КПД имеет в качестве нагревателя резервуар с кипящей водой при 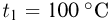 , а в качестве холодильника — сосуд со льдом при
, а в качестве холодильника — сосуд со льдом при 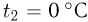 . Какая масса льда m растает при совершении машиной работы
. Какая масса льда m растает при совершении машиной работы 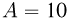 Дж? Удельная теплота плавления льда
Дж? Удельная теплота плавления льда 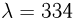 Дж/г.
Дж/г.
Решение:
Максимально возможный КПД достигается, если тепловая машина работает по циклу Карно. Он равен 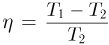 , где
, где 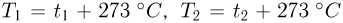 — абсолютные температуры нагревателя и холодильника. С другой стороны, по определению КПД
— абсолютные температуры нагревателя и холодильника. С другой стороны, по определению КПД 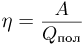 , где
, где 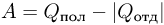 — работа газа за цикл,
— работа газа за цикл, 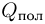 — количество теплоты, полученное за цикл от нагревателя,
— количество теплоты, полученное за цикл от нагревателя, 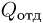 — количество теплоты, отданное за цикл холодильнику. Из равенства
— количество теплоты, отданное за цикл холодильнику. Из равенства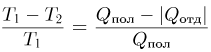
находим, что 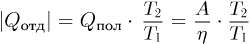 . Отданная холодильнику теплота расходуется на таяние льда при температуре плавления. Следовательно,
. Отданная холодильнику теплота расходуется на таяние льда при температуре плавления. Следовательно, 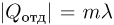 . Объединяя записанные выражения, получаем ответ:
. Объединяя записанные выражения, получаем ответ: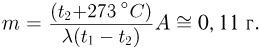
Задача №6.18.
Объем тонкостенного цилиндрического сосуда высотой 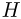 = 40 см равен
= 40 см равен 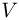 = 400 см3, его вес
= 400 см3, его вес 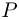 = 3,3
= 3,3 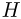 . При температуре
. При температуре 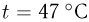 и атмосферном давлении
и атмосферном давлении 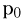 = 100 кПа сосуд переворачивают вверх дном и погружают в жидкость плотностью
= 100 кПа сосуд переворачивают вверх дном и погружают в жидкость плотностью 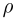 = 1000
= 1000 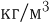 . При какой температуре
. При какой температуре 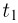 сосуд утонет? Атмосферное давление считать неизменным, ускорение свободного падения принять
сосуд утонет? Атмосферное давление считать неизменным, ускорение свободного падения принять 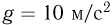 .
.
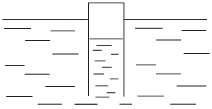
Решение:
При понижении температуры объем воздуха в сосуде уменьшается и он погружается в воду. Сосуд будет оставаться на плаву до тех пор, пока его дно не окажется на одном уровне с поверхностью воды. Силы, действующие на сосуд, при этом еще будут уравновешены. При дальнейшем понижении температуры равновесие сил станет невозможным, и сосуд начнет тонуть. Это произойдет из-за того, что объем воздуха в сосуде и, следовательно, архимедова сила еще больше уменьшатся, а сила, действующая вниз на дно сосуда, увеличится, поскольку к силе давления атмосферного воздуха добавится сила давления воды на дно.
Исходя из этих рассуждений, рассмотрим случай, когда сосуд еще плавает, но его дно уже находится вровень с поверхностью воды. Обозначим через 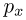 давление воздуха в сосуде, а через
давление воздуха в сосуде, а через 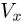 — объем воздуха. Учитывая, что площадь сечения сосуда
— объем воздуха. Учитывая, что площадь сечения сосуда 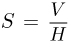 , запишем условие равновесия сосуда под действием приложенных к нему сил:
, запишем условие равновесия сосуда под действием приложенных к нему сил:
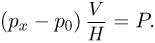
Из закона Архимеда следует, что
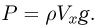
Из этих равенств легко найти 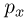 и
и 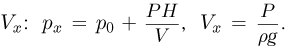 Уравнения начального и конечного состояния воздуха в сосуде имеют вид:
Уравнения начального и конечного состояния воздуха в сосуде имеют вид:
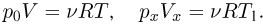
Отсюда 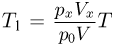 . Подставляя сюда найденные
. Подставляя сюда найденные 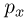 и
и 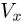 , получаем ответ:
, получаем ответ: 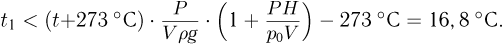
Задача №6.19.
Заряженная частица движется в однородном электрическом поле напряженностью 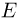 = 30 В/м. Известно, что в момент, когда кинетическая энергия частицы достигает минимума, ее скорость направлена под углом
= 30 В/м. Известно, что в момент, когда кинетическая энергия частицы достигает минимума, ее скорость направлена под углом 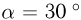 к горизонту. Определить разность потенциалов
к горизонту. Определить разность потенциалов 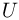 между точками
между точками 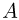 и
и 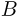 поля, лежащими на одной горизонтали на расстоянии
поля, лежащими на одной горизонтали на расстоянии 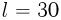 см друг от друга. Действием силы тяжести пренебречь.
см друг от друга. Действием силы тяжести пренебречь.
Решение:
Из курса механики известно, что траектория тела, движущегося под действием постоянной по величине и по направлению силы, представляет собой в общем случае параболу. Такое движение полностью аналогично движению тела, брошенного под углом к горизонту вблизи поверхности Земли. Пользуясь этой аналогией, легко установить, что кинетическая энергия тела принимает минимальное значение в точке, в которой скорость тела перпендикулярна действующей на него силе, в нашем случае в точке, где 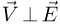 (см. рисунок).
(см. рисунок).
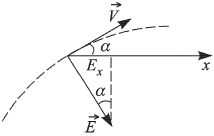
Тем самым направление напряженности электрического поля в пространстве определено. Проекция напряженности поля на горизонтальную ось 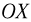 равна
равна 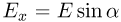 . Поскольку искомая разность потенциалов определяется как
. Поскольку искомая разность потенциалов определяется как 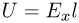 ответ имеет вид:
ответ имеет вид:
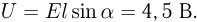
Задача №6.20.
Автомобиль, движущийся по горизонтальной дороге, попадает в полосу дождя, капли которого падают на землю вертикально с постоянной скоростью. Известно, что при скорости автомобиля 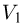 = 36 км/час в его наклонное лобовое стекло попадает
= 36 км/час в его наклонное лобовое стекло попадает 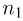 = 200 дождевых капель в секунду, а при скорости
= 200 дождевых капель в секунду, а при скорости 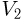 = 72 км/час это число возрастает до
= 72 км/час это число возрастает до 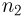 = 300 капель в секунду. Сколько капель
= 300 капель в секунду. Сколько капель 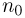 будет попадать в лобовое стекло за 1 секунду, если автомобиль остановится?
будет попадать в лобовое стекло за 1 секунду, если автомобиль остановится?
Решение:
Используя рассуждения, проводимые при выводе основного уравнения молекулярно — кинетической теории идеального газа, находим, что число капель, попадающих за 1 секунду на ветровое стекло автомобиля, 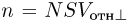 , где
, где 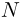 — число капель в единице объема,
— число капель в единице объема, 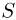 — площадь стекла,
— площадь стекла, 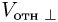 — проекция скорости капель относительно автомобиля на нормаль к стеклу. По закону сложения скоростей
— проекция скорости капель относительно автомобиля на нормаль к стеклу. По закону сложения скоростей 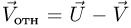 , где
, где 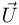 и
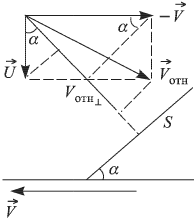
и 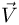 — скорости капель и автомобиля относительно земли (см. рисунок). Обозначив через
— скорости капель и автомобиля относительно земли (см. рисунок). Обозначив через 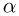 угол наклона ветрового стекла и используя известное из геометрии утверждение о том, что проекция суммы векторов на какое-либо направление равна сумме проекций векторов на это направление, находим, что
угол наклона ветрового стекла и используя известное из геометрии утверждение о том, что проекция суммы векторов на какое-либо направление равна сумме проекций векторов на это направление, находим, что 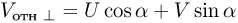 . Следовательно, справедливы следующие равенства:
. Следовательно, справедливы следующие равенства:
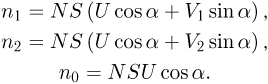
Умножая первое соотношение на 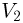 , а второе на
, а второе на 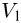 и вычитая одно из другого, получаем:
и вычитая одно из другого, получаем:
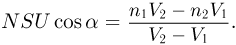
Ответ: 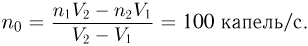
Задача №6.21.
Шарик массой 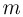 = 7,2 г, несущий заряд
= 7,2 г, несущий заряд 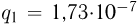 Кл, подвешен на невесомой, нерастяжимой и непроводящей нити длиной
Кл, подвешен на невесомой, нерастяжимой и непроводящей нити длиной 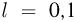 м и вращается с постоянной угловой скоростью, причем угол между нитью и вертикалью
м и вращается с постоянной угловой скоростью, причем угол между нитью и вертикалью 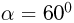 . В центре окружности, по которой движется шарик, расположен точечный заряд
. В центре окружности, по которой движется шарик, расположен точечный заряд 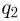 =
= 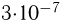 Кл. Найти угловую скорость вращения шарика
Кл. Найти угловую скорость вращения шарика 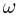 . Электрическая постоянная
. Электрическая постоянная 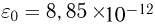 Ф/м. Ускорение свободного падения принять
Ф/м. Ускорение свободного падения принять 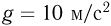 , размером шарика пренебречь.
, размером шарика пренебречь.
Решение:
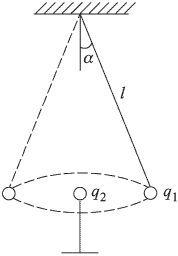
Для решения задачи будем использовать неподвижную систему координат, плоскость 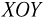 которой в некоторый момент времени совпадает с плоскостью, проходящей через ось вращения системы и нить с шариком (см. рисунок).
которой в некоторый момент времени совпадает с плоскостью, проходящей через ось вращения системы и нить с шариком (см. рисунок).
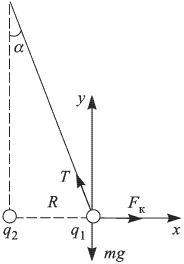
Поскольку шарик совершает равномерное движение по окружности, его ускорение направлено к ее центру и по величине равно 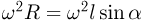 . Движение шарика происходит под действием трех сил: силы тяжести
. Движение шарика происходит под действием трех сил: силы тяжести 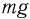 , силы натяжения нити
, силы натяжения нити 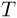 и силы электрического взаимодействия между зарядами (кулоновской силы)
и силы электрического взаимодействия между зарядами (кулоновской силы) 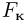 . В проекциях на координатные оси выбранной системы имеем:
. В проекциях на координатные оси выбранной системы имеем:
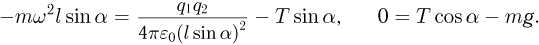
Исключая отсюда натяжение нити 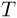 , после несложных преобразований получаем ответ:
, после несложных преобразований получаем ответ: 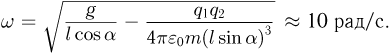
Задача №6.22.
В лифте, движущемся с ускорением 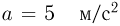 , направленным вверх, находится цилиндрический сосуд, закрытый поршнем массой
, направленным вверх, находится цилиндрический сосуд, закрытый поршнем массой 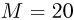 кг и площадью
кг и площадью 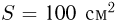 . Под поршнем находится идеальный газ. Поршень расположен на расстоянии
. Под поршнем находится идеальный газ. Поршень расположен на расстоянии 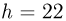 см от дна сосуда. Определить, на какую величину
см от дна сосуда. Определить, на какую величину 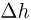 переместится поршень, если лифт будет двигаться с тем же по модулю ускорением, направленным вниз. Температура газа не изменяется. Атмосферное давление
переместится поршень, если лифт будет двигаться с тем же по модулю ускорением, направленным вниз. Температура газа не изменяется. Атмосферное давление  Па, ускорение свободного падения принять
Па, ускорение свободного падения принять 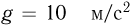 . Трением поршня о стенки сосуда пренебречь.
. Трением поршня о стенки сосуда пренебречь.
Решение:
Поршень, покоящийся в движущемся лифте, имеет относительно неподвижной системы отсчета ускорение а, совпадающее с ускорением лифта. Запишем уравнения движения поршня в проекциях на направление его ускорения:
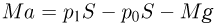 при ускорении
при ускорении 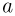 , направленном вверх,
, направленном вверх,
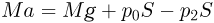 при ускорении
при ускорении 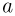 , направленном вниз.
, направленном вниз.
Здесь 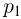 и
и 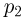 — давления газа под поршнем в этих случаях. Из уравнения состояния газа под поршнем следует, что
— давления газа под поршнем в этих случаях. Из уравнения состояния газа под поршнем следует, что
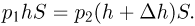
Решая эту систему уравнений, находим ответ:
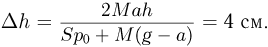
Задача №6.23.
Два маленьких тела начинают одновременно соскальзывать без начальной скорости из точки 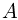 : первое по внутренней поверхности гладкой сферы до ее нижней точки
: первое по внутренней поверхности гладкой сферы до ее нижней точки 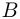 , второе по гладкой наклонной плоскости
, второе по гладкой наклонной плоскости 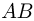 .
.
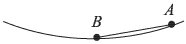
Пренебрегая трением найти, во сколько раз 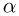 отличаются времена движения этих тел от начальной до конечной точек. Расстояние
отличаются времена движения этих тел от начальной до конечной точек. Расстояние 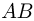 намного меньше радиуса сферы.
намного меньше радиуса сферы.
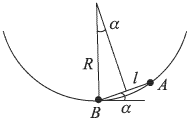
Решение:
Поскольку расстояние между точками 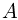 и
и 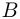 намного меньше радиуса сферы, можно считать, что тело, скользящее по гладкой сферической поверхности радиусом
намного меньше радиуса сферы, можно считать, что тело, скользящее по гладкой сферической поверхности радиусом 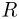 , движется как математический маятник длиной
, движется как математический маятник длиной 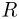 , совершающий малые колебания. Поэтому время его движения из точки
, совершающий малые колебания. Поэтому время его движения из точки 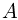 в точку
в точку 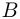 равно четверти периода
равно четверти периода 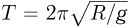 колебаний маятника, т.е.
колебаний маятника, т.е.
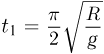
Тело на гладкой наклонной плоскости, составляющей угол 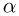 с горизонталью, движется с ускорением
с горизонталью, движется с ускорением 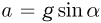 . Длина наклонной плоскости совпадает с расстоянием между точками
. Длина наклонной плоскости совпадает с расстоянием между точками 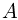 и
и 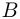 , которое, как видно из рисунка, равно
, которое, как видно из рисунка, равно 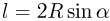 . Следовательно, время движения этого тела из точки
. Следовательно, время движения этого тела из точки 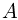 в точку
в точку 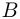
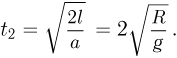
Ответ: 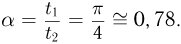
Задача №6.24.
Брусок расположен на гладкой горизонтальной плоскости и соединен горизонтальной пружиной жесткостью 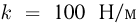 с вертикальной стенкой. Перпендикулярно поверхности бруска летят капли воды массой
с вертикальной стенкой. Перпендикулярно поверхности бруска летят капли воды массой 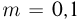 г каждая со скоростью
г каждая со скоростью 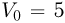 м/с.
м/с.
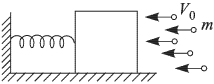
Ударившись о брусок, капли, не отскакивая от него, стекают на землю. Найти, на какую величину 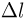 сжимается пружина, если известно, что брусок не совершает колебаний. Число капель в единице объема потока
сжимается пружина, если известно, что брусок не совершает колебаний. Число капель в единице объема потока 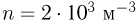 . Площадь поверхности бруска, в которую ударяют капли,
. Площадь поверхности бруска, в которую ударяют капли, 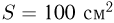 .
.
Решение:
Ударяющиеся о поверхность бруска капли воды оказывают на нее давление подобно тому, как оказывают давление на стенку сосуда молекулы находящегося в нем газа. Поэтому для решения задачи можно воспользоваться приемами, применяемыми для вывода основного уравнения молекулярно — кинетической теории идеального газа, с той лишь разницей, что соударения капель с поверхностью бруска являются неупругими и все капли, в отличие от молекул газа, летят с одной и той же скоростью.
Изменение импульса одной капли при ударе о поверхность неподвижного бруска равно:
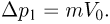
За время 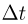 в брусок ударяется
в брусок ударяется 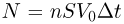 капель. Следовательно, величина импульса силы давления капель на поверхность бруска за время
капель. Следовательно, величина импульса силы давления капель на поверхность бруска за время 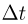 равна:
равна:
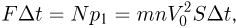
а величина самой силы давления есть 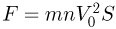 . Под действием этой силы брусок смещается на некоторое расстояние
. Под действием этой силы брусок смещается на некоторое расстояние 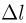 , сжимая пружину. Возникающая в пружине сила упругости, величина которой
, сжимая пружину. Возникающая в пружине сила упругости, величина которой 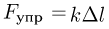 , уравновешивает силу давления капель:
, уравновешивает силу давления капель: 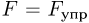 . Объединяя записанные соотношения, получаем ответ:
. Объединяя записанные соотношения, получаем ответ: 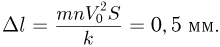
Задача №6.25.
Шарик массой 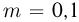 г, несущий отрицательный заряд
г, несущий отрицательный заряд 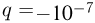 Кл, движется по силовой линии однородного электрического поля с напряженностью
Кл, движется по силовой линии однородного электрического поля с напряженностью 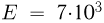 В/м, направленной вертикально вниз. На пути
В/м, направленной вертикально вниз. На пути 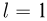 м величина скорости шарика изменилась в 2 раза, а направление скорости осталось неизменным. Найти величину скорости шарика
м величина скорости шарика изменилась в 2 раза, а направление скорости осталось неизменным. Найти величину скорости шарика 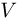 в конце этого пути. Ускорение свободного падения принять
в конце этого пути. Ускорение свободного падения принять 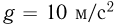 . Сопротивлением воздуха пренебречь.
. Сопротивлением воздуха пренебречь.
Решение:
Шарик движется под действием двух сил: силы тяжести и кулоновской силы, причем последняя направлена против электрического поля, поскольку заряд шарика отрицательный. В проекции на вертикальную координатную ось, направленную вниз, суммарная сила, действующая на шарик, равна:
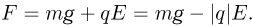
На перемещении 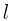 эта сила совершает работу
эта сила совершает работу 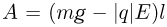 . По условию задачи шарик движется по полю, т.е. вниз, и на рассматриваемом отрезке пути его скорость не меняет своего направления. Следовательно, перемещение шарика положительно. В соответствии с законом изменения кинетической энергии тела,
. По условию задачи шарик движется по полю, т.е. вниз, и на рассматриваемом отрезке пути его скорость не меняет своего направления. Следовательно, перемещение шарика положительно. В соответствии с законом изменения кинетической энергии тела,
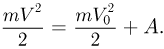
где 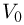 — скорость шарика в начале рассматриваемого пути,
— скорость шарика в начале рассматриваемого пути, 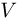 — его скорость в конце этого пути. Из последнего соотношения находим:
— его скорость в конце этого пути. Из последнего соотношения находим:
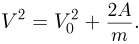
Очевидно, что ответ зависит от знака работы, который определяется знаком проекции суммарной силы, действующей на шарик, на выбранную координатную ось. Таким образом, если сила тяжести больше кулоновской силы, то 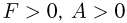 , и скорость шарика увеличивается в два раза
, и скорость шарика увеличивается в два раза 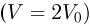 , при этом равенство (25) принимает вид:
, при этом равенство (25) принимает вид: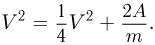
В противном случае 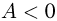 и скорость шарика уменьшается в два раза
и скорость шарика уменьшается в два раза 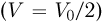 ; тогда (25) следует:
; тогда (25) следует:
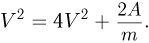
Объединяя записанные соотношения, получаем ответ:
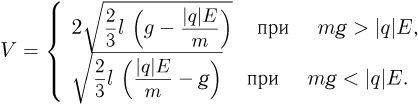
Подстановка численных данных из условия задачи дает для конечной скорости значение 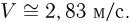
Задача №6.26.
На шероховатом столе лежит доска массой 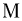 = 1 кг и длиной
= 1 кг и длиной 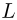 = 0,5 м так, что за край стола выступает ее часть длиной
= 0,5 м так, что за край стола выступает ее часть длиной 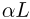 , где
, где 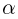 = 1/4.
= 1/4.
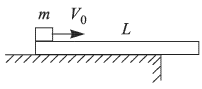
Какую минимальную скорость 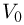 нужно сообщить маленькому бруску массой
нужно сообщить маленькому бруску массой 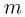 = 1 кг, находящемуся на левом конце доски, чтобы в результате его перемещения левый конец доски приподнялся над столом?
= 1 кг, находящемуся на левом конце доски, чтобы в результате его перемещения левый конец доски приподнялся над столом?
Коэффициент трения между бруском и доской 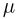 = 0, 1. Доска при движении бруска не скользит по столу. Толщиной доски пренебречь, ускорение свободного падения принять
= 0, 1. Доска при движении бруска не скользит по столу. Толщиной доски пренебречь, ускорение свободного падения принять 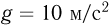 .
.
Решение:
Доска, лежащая на столе, взаимодействует с ним во всех точках соприкосновения.
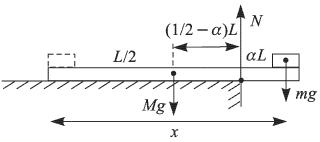
Элементарные силы упругости, действующие со стороны стола на каждый элемент нижней поверхности доски, имеют равнодействующую, величина которой равна суммарному весу доски и кубика, а точка приложения определяется из уравнения моментов. Эту равнодействующую часто называют силой реакции стола. При движении кубика по доске точка приложения силы реакции стола перемещается вправо до тех пор, пока не достигнет его края. В этот момент левый конец доски перестает давить на стол. Дальнейшее перемещение кубика приведет к тому, что доска опрокинется через край стола.
Силы, действующие на доску в момент, когда ее левый конец перестает давить на стол, изображены на рисунке. Из уравнения моментов, записанного относительно оси, проходящей по краю стола, получаем:
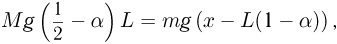
где 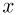 — смещение кубика от начального положения. Для того, чтобы связать смещение
— смещение кубика от начального положения. Для того, чтобы связать смещение 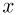 с начальной скоростью кубика
с начальной скоростью кубика 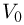 , воспользуемся законом изменения кинетической энергии тела, согласно которому
, воспользуемся законом изменения кинетической энергии тела, согласно которому
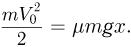
Отсюда 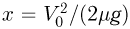 . Объединяя это выражение с первым, находим ответ:
. Объединяя это выражение с первым, находим ответ: 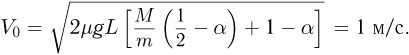
Задача №6.27.
На гладком горизонтальном столе лежит деревянный брусок, прикрепленный пружиной к вертикальной стенке. В брусок попадает пуля массой 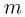 = 10 г, летящая горизонтально вдоль оси пружины, и застревает в нем.
= 10 г, летящая горизонтально вдоль оси пружины, и застревает в нем.
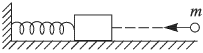
Определить жесткость пружины 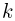 , если известно, что время, в течение которого сжималась пружина после попадания пули в брусок,
, если известно, что время, в течение которого сжималась пружина после попадания пули в брусок, 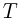 = 0, 1 с, отношение количества теплоты, выделившейся при взаимодействии пули с бруском, к начальной кинетической энергии пули
= 0, 1 с, отношение количества теплоты, выделившейся при взаимодействии пули с бруском, к начальной кинетической энергии пули 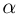 = 0,9. Трением бруска о стол, а также массой пружины пренебречь.
= 0,9. Трением бруска о стол, а также массой пружины пренебречь.
Решение:
Обозначим через 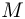 массу бруска. Из закона сохранения импульса и закона изменения механической энергии следуют равенства:
массу бруска. Из закона сохранения импульса и закона изменения механической энергии следуют равенства:
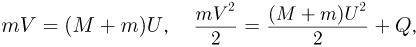
где 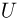 — скорость пули и бруска после соударения,
— скорость пули и бруска после соударения, 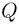 — количество теплоты, выделившееся при взаимодействии пули с бруском, причем по условию
— количество теплоты, выделившееся при взаимодействии пули с бруском, причем по условию 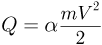 . Время
. Время 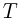 , в течение которого сжималась пружина, равно четверти периода колебаний тела массой
, в течение которого сжималась пружина, равно четверти периода колебаний тела массой 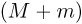 на пружине жесткостью
на пружине жесткостью 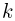 , т.е.
, т.е.
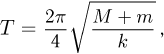
Объединяя записанные выражения, после несложных преобразований получаем ответ: 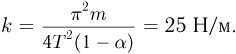
Задача №6.28.
Вертикально расположенная цилиндрическая теплоизолированная трубка диаметром 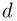 = 1 см, закрытая подвижным невесомым поршнем, содержит идеальный одноатомный газ. Внутри трубки содержится резистор с большим сопротивлением, соединенный через ключ с конденсатором емкостью
= 1 см, закрытая подвижным невесомым поршнем, содержит идеальный одноатомный газ. Внутри трубки содержится резистор с большим сопротивлением, соединенный через ключ с конденсатором емкостью 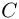 = 1 мкФ, заряженным до напряжения
= 1 мкФ, заряженным до напряжения 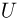 = 200 В.
= 200 В.
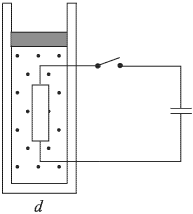
Подводящие провода имеют ничтожно малое сопротивление и не нарушают герметичность трубки. На какое расстояние 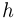 поднимется поршень после замыкания ключа и установления теплового равновесия? Атмосферное давление
поднимется поршень после замыкания ключа и установления теплового равновесия? Атмосферное давление 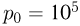 Па.
Па.
Решение:
При разрядке конденсатора в резисторе выделится количество тепла, равное первоначальной энергии конденсатора:
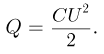
Поскольку давление газа в трубке постоянно и равно 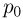 ,
,
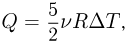
где 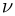 — количество газа,
— количество газа, 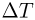 — изменение его температуры. Из уравнения изобарного процесса следует, что
— изменение его температуры. Из уравнения изобарного процесса следует, что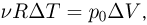
где 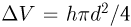 — изменение объема газа. Объединяя записанные выражения, получаем ответ:
— изменение объема газа. Объединяя записанные выражения, получаем ответ: 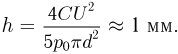
Возможно эти дополнительные страницы вам будут полезны:
- Предмет физика
- Готовые задачи по физике
- Решение задач по физической механике
- Заказать работу по физике
- Помощь по физике
- Решение задач по молекулярной физике
- Решение задач по электростатике и электродинамике
- Постоянный ток задачи с решением
- Магнетизм задачи с решением
- Электромагнитные колебания задачи с решением
- Задачи по оптике с решением

