




- Типичное сопло Лаваля показано на рисунке. 17. 5. Характер движения в насадке зависит от того, хотите ли вы достичь скорости звука или скорости питомца. Дозвуковой поток. P3 равно p0 (индекс показан на рисунке 17. 5), сопло не имеет никакого движения. если pa немного меньше p0, то поток в сопле качественно аналогичен тому, который уже изучался в разрезе 6 вниз по течению Вентури. Давление падает и скорость падает 1 в оригинале используется термин sopuegvtd — ^ wgddt t1O2r1e. In в этом переводе был введен термин «сопло Лаваля», который является общепринятым. (Прим, перев.) Сопло Лаваль. Здесь скорость есть. Тогда его максимум Уравнение 17.
До предела I, затем давление начинает увеличиваться, а скорость уменьшается, пока не достигнет выходного сечения 3\, и давление p8 и p4 равны equal. In узкие участки, все точки измерения имеют экстремумы. Это и BC6 эквивалентно нулю. Поэтому он заполняется (17.1), а также всей насадкой. Сверхзвуковой поток. Снижение давления Р3 увеличивает максимальную скорость, которая достигается в узкой части сопла. Значение, которое может быть достигнуто, равно скорости звука при температуре газа в камере. Isthmus. To влияние на состояние точки, в которой изменение давления на выходе находится выше по потоку, возмущение давления Вам нужно отправить его в восходящий поток.
Изменения давления распространяются влево со скоростью звука, поэтому, если правая скорость газа достигает скорости звука в какой-то момент, дальнейшее продвижение волны давления останавливается. При дозвуковом истечении достигается максимальный рост звука, так как скорость сужения 1 сопла больше, чем в любой другой точке.
Когда давление на выходе падает Давление падает ниже этого уровня ^ chesh, от от Чили для » связи C03 SK ° Р°8 STI критический звук, никакое давление не передается в этом разделе. И» путь » >условие между разделом 0 и I остается без давления LeGK°(1 /.17), а значение P / равно C или〜 Гора’ Расчет (17. Двадцать два) cheskoeDsechenleGP (АП ^ OaCher?* IX) всего Чищв Фити — » как иереводится° Что касается газа, то, как правило, незначительно превышает 0,5.Обратите внимание, что максимальная скорость (и/ = Ce) критической секции меньше скорости звука во входном условии (Co).Формула (17. И), (17.12) и 17.
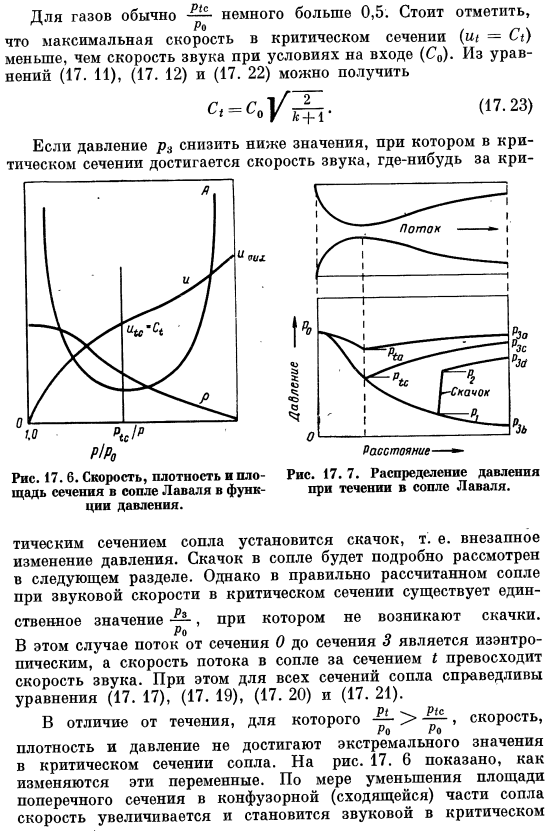
Можно получить следующую формулу: Если давление p3 падает ниже значения, достигающего скорости звука в критическом сечении、 17.6.Скорость, плотность и площадь поперечного сечения сопла Лаваля в зависимости от давления. 17. 7.Распределение давления в потоке в сопле Лаваля. Поперечное сечение сопла устанавливает скачок, то есть внезапное изменение давления. Скачок сопла подробно описан в следующем разделе. Однако правильно рассчитанное сопло при скорости звука в критическом сечении имеет единственное значение, которое не вызывает jump.
В этом случае поток из секции 0 в секцию 3 является изоэнтропийным, а скорость потока в сопле после секции I-превышает скорость звука. Далее, для всех секций сопла формула(17. 17), (17.19), (17.20), и (17. 21) действует. В отличие от скорости тока、 Плотность и давление не достигают экстремальных значений в критическом сечении сопла.17. 6 показывает изменения в них variables. As площадь поперечного сечения уменьшается в сходящейся (сходящейся) части сопла, увеличивается скорость и звук в критической section. In расходящаяся часть сопла, скорость продолжает увеличиваться, а давление уменьшается. Рисунок из 17.
Для некоторого P6 между p c и 0 существует только значение A3 (то есть 1 сопло), и поток без скачков возможен. независимо от того, что k4k является большим, существует конечный предел скорости. Его величина определяется по формуле (17. 17) можно найти, подставив p = 0. На рисунке показан характер изменения давления вдоль сопла. 17. 7.Если rz достаточно велик, чтобы скорость звука не достигала нигде на сопле, вы получаете кривую, которая достигает paa.
Скачок образуется за критическим сечением сопла, когда скорость звука достигается в P, c критического сечения и немного медленнее, чем ccb, но не равна. с достижением пбд поток становится сверхзвуковым на всей расходящейся части сопла Как следует из графика на рисунке 17. 6 и 17. 7, сокращая сопло так, что 33 будет уменьшено, pzb увеличат.
Если вы укоротили сопло так, что осталась только сходящаяся часть сопла, pb-pcc = p, c; если в сопле нет расширяющейся части, она не может превышать скорость звука. Вот еще один способ показать, что вам нужно достичь скорости звука, как только вы получите p3 pcc в критическом разделе. Формула.(А если нет скачка на сопле, то по следующей формуле (17. 17) всегда заполняется. для p3 > Rzs скорость звука не достигается, и, как мы видели, следующая форма уравнения баланса масс ИК Ил б / р 4-РЛ = 0(17.24) Удовлетворен критической секцией, здесь&a = 0 И ai также равен нулю. Однако, для Р3 rzc, разность потенциалов не равна нулю, и поэтому в критической секции, формула 17.
Представляет собой формулу (17. 5) воля be. As уже указано, что уравнение(17. 5) и (17. 6) есть и другие доказательства того, что эта скорость в p3 p, c должна быть достигнута в критическом сечении, так как совместное решение дает формулу скорости звука. Плинтус сопла Давайте еще раз вернемся к фигуре. 17. 5 и 17. 7, и рассмотрим, что произойдет, если p4 меньше p3, но не равно p3.
- Если p4 меньше mr, давление в сопле следует кривой, ведущей к pb, то сразу после сопла поток быстро расширяется, образуя систему осевых ударных волн (скачков), показанную на рисунке 5. 17.8 A. Если размах значительно больше rz, выходящего из сопла, то в потоке образуется система ударных волн и происходит сжатие при расширении сопла°Dal » 4, входящем в 3 из 3 рассмотренных случаев. Анализ.
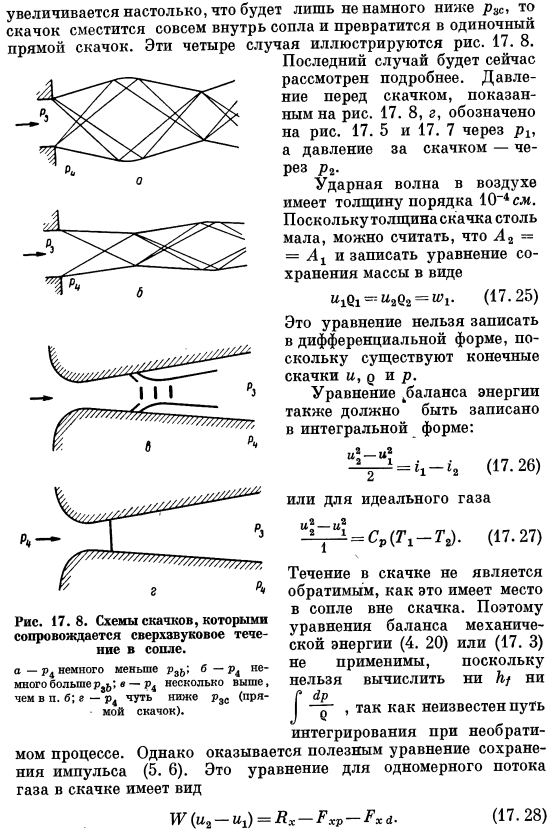
Обычно, чем немного ниже РЗС, тем больше он, прыжок будет полностью двигаться в сопле, превращаясь в один прямой прыжок. Эти 4 случая показаны на рисунке. 17.8. Последнее дело сейчас Мы рассмотрели его более подробно. Давление перед прыжком показано на рисунке. Рис.17. 8а 17. 5 и 17. 7 P2 после прыжка через давление. Толщина ударной волны в воздухе составляет порядка 1 0 4f. так как толщина удара очень мала, то можно принять A2 — =и описать уравнение сохранения массы в следующем виде: «121v8M12″=«, 1 — (17.25) Поскольку существуют конечные скачки u, p, p, это уравнение не может быть описано в дифференциальной форме.
Уравнение энергетического баланса^также должно быть записано в целочисленной форме. И2-И2 (17.26) Рис. 17.8.Скачкообразная картина, сопровождающая сверхзвуковой поток в сопле. a-p4 немного меньше, чем p8& b-p4 немного больше, чем 8& c-p4 немного выше, чем пункт B. p4 (прямой прыжок) чуть ниже r-rzs. Мамин процесс. Однако импульс импульса (5. 6). Оказывается. Это Уравнение Форма газа в прыжке Или для идеального газа ^ 1 =Вода (7 ′ 1-T2)-(17.27) Как и в случае внешнего сопла удара, поток удара не является обратимым. Следовательно, баланс механической энергии (4. 20) или (17. 3) не применимо.
Уравнение сохранения для 1-мерного потока, потому что интегральный путь бесполезного неизвестен Ж(и2-и1)=Вх-Рхр—Гха. (17. 28) стенка сопла не входит в управляющий объем, поэтому усилие Нх будет равно нулю. Мощность PxL может быть установлена на ноль. Это связано с тем, что длина управляющего объема коротка, поэтому силой трения о стенки можно пренебречь. Результирующая сила давления равна Al (p, — пЛ и и7 = 、 «121 („2 -“ х)= — Р2. (17. 29.) Уравнение 17.
Используя соответствующую термодинамическую формулу идеального газа, можно получить следующее простое соотношение для связи скоростей обеих сторон ударной волны(вывод этого уравнения связан с длительными и сложными расчетами) ): „1“ 2 = C?。 (17.30) Скорость превышает скорость звука, а скорость and2, как вы можете видеть, медленнее скорости звука. Этот факт уже используется при построении фигуры. 17. 7 графиков, заканчивающихся давлением rzL. Давление в расширительной части сопла увеличивается с дозвуковым истечением и уменьшается со сверхзвуковым истечением. (17. 30) вместо выполнения алгебраических вычислений, приводящих к уравнению (17. 26) и 17.
Показана иллюстрация совместного решения. (17. 25), исключают скорость из этих уравнений и (17.26). И от (17.29) и ’ 2 Два Мне 21а) Х- (17. Тридцать одна) / 1 1 \ 2 и ее-П1-п- (Индекс 2 этих уравнений опущен.) Чтобы использовать эти уравнения, укажите, при каком давлении или скорости это происходит до прыжка.
Если P1 известен, то это u1> e1, и последующие журналы вычисляются с использованием уже рассмотренной доли потока изэнтропии между секциями 0 и 1.Поэтому мое решение Mo ^ p°определяет точки На рисунке I-8 (рисунок 17 рисунок 61 рисунок) ’ TaK tq0 количество w> $ 1 и A также известны. В этом случае выберите непрерывное значение o и вычислите соответствующее значение r из точки выравнивания. Называется lInLP0Ka3aNpUYu, а Faino — это » 17 ″ 9 кривая риса называется. Аналогично, вы можете использовать набор задач Vvenem (1-7 ’32) ’для вычисления и p, который определяет кривую, называемую линией.
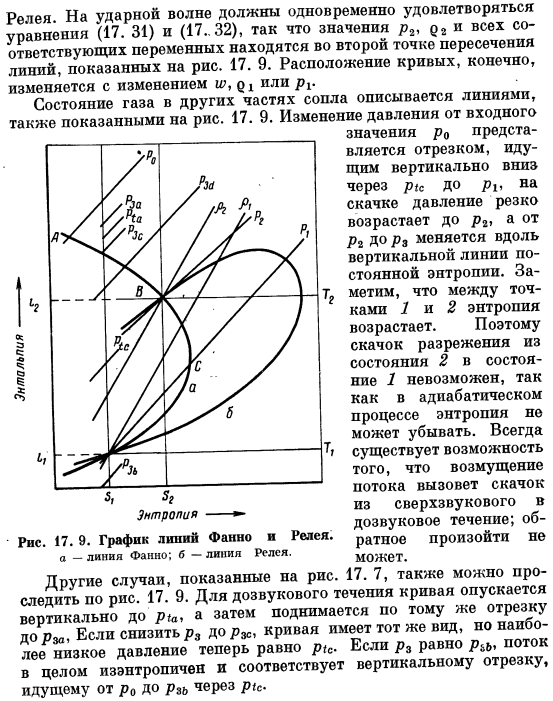
Тридцать два. Поскольку вы знаете прыжок 1 ″ p 1>, Вы можете: в соотношении ударная волна Рэлея, уравнение (17. 31) и (17. 32) должны быть удовлетворены в то же время, значения p2, p2 и все соответствующие переменные находятся на 2-м пересечении. Линия, показанная на рисунке 17. 9.Расположение кривых, конечно, изменилось или ру Состояние газа в других частях сопла представлено линией, показанной на рисунке 1. 17. 9.Изменение давления от входа 17. 9.График линии Рэлея с линией ФАНО. И _ _ _ _ линия Фанно; Б-линия Рэлея.
Газовое состояние других частей сопла величина p0 представлена отрезком, который при ударе опускается перпендикулярно к Пу через ри, а давление резко возрастает до p2, изменяясь вдоль вертикальной линии постоянной энтропии от Pch к Pz. Обратите внимание, что энтропия увеличивается между точками 1 и 2.Таким образом, скачок разрежения из состояния 2 в состояние 1 невозможен, поскольку адиабатический процесс не может уменьшить энтропию. Всегда существует вероятность того, что возмущение потока вызывает скачок от сверхзвукового к дозвуковому.
Обратного произойти не может. Другие случаи показаны на рисунке. 17. 7, также возможно следовать диаграммой. 17. 9.In в случае дозвукового течения, когда p3 уменьшается до Rzs, кривая спускается вертикально вниз до p1a, затем вдоль того же сегмента и до pm. Кривые имеют одинаковую форму, и самое низкое давление равно p c.
Смотрите также:
