

- Приведенные ниже комментарии относятся только к турбулентности. Некоторые случаи ламинарного течения ч. 12. Диаграмма 15. 1 и 15. 5 можно использовать для турбулентного течения различных некруглых труб, заменяя диаметр Р эквивалентным диаметром 2) ЭКП. (15.4) Гидравлический радиус rn, который входит в это уравнение, определяется по формуле: (15.5) Здесь 1P-это влажная граница трубы. А-площадь поперечного сечения трубки.
В случае круглых труб можно подтвердить, что эти определения следуют результату ReKv = = R. например, для перемещения с кольцевым зазором Req = » — Так мы получаем: (15.6) И Не= И затем (15. Семь) При заданном гидравлическом радиусе таким образом график коэффициента сопротивления может быть использован для открытых каналов и потока плохо заполненных труб 1 2. Ваш 8 исследовал поток вокруг цилиндра; количественные результаты показаны на графике. 8.9. Ваш 14 график 8.
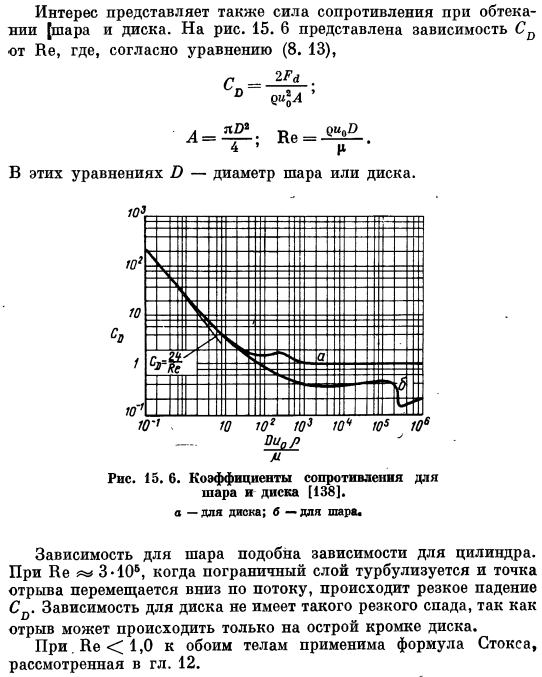
- Показано, что тип переменной, подлежащей построению, может быть установлен с помощью размерного анализа. 1. Более простым методом является анализ графов, состоящий из построения левой и правой частей формулы (6)в функцию Dpx и определения по их точкам пересечения. (Примечание, редактировать) 2 Вообще говоря, форма сечения также влияет на гидравлическое сопротивление, но главным определяющим размером является гидравлический радиус. (Примечание, редактировать) Интересным является перетаскивание вокруг шара и диска. Рис.15. 6 показана зависимость Св * ть. Где формула(8. 13) Согласно. 2Pa 0 Ци * А ’ Д Рис.15. 6.Коэффициент сопротивления шариков и дисков[138]. А потом-за диск; б-за мяч.
Зависимость от шара аналогична зависимости от цилиндра. В BE3 * 106, когда пограничный слой турбулентен и точка разделения движется вниз по течению, Co резко падает. Разделение происходит только на острых краях диска, поэтому зависимость от диска не падает так резко. В. 1.0, уравнения Стокса рассматриваются в разделе.
Смотрите также:
